|
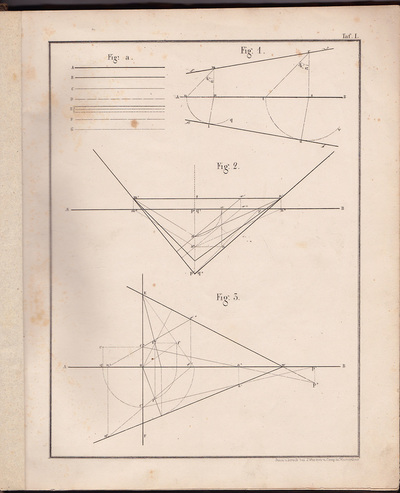
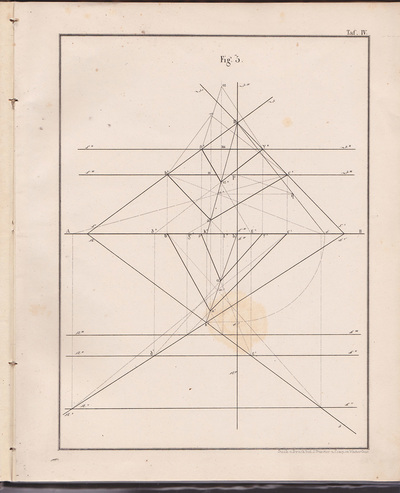
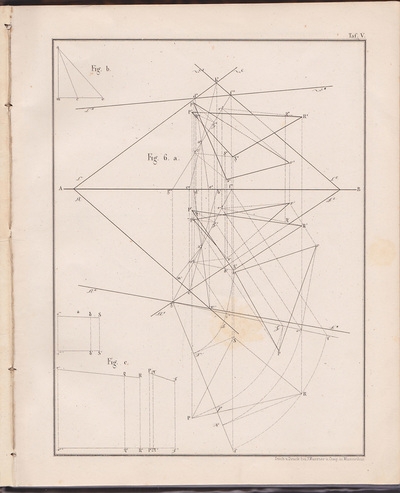
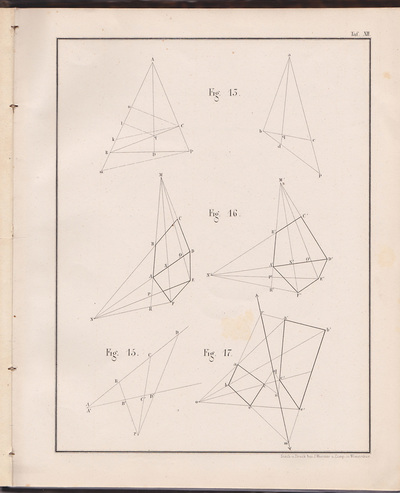
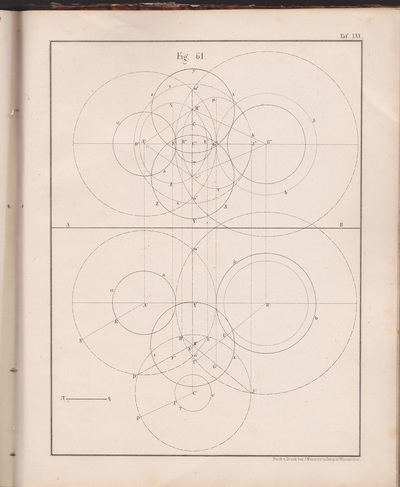
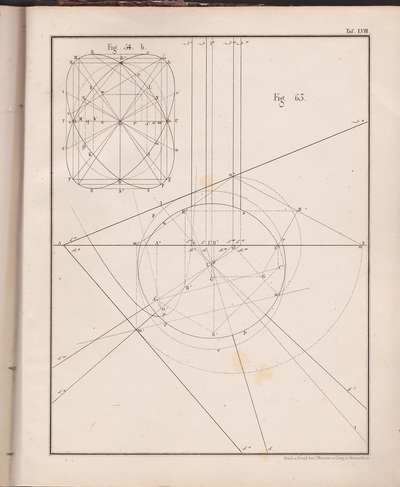
❉ This is the eighth in a series of blogs that discuss diagrams and the diagrammatic format, especially in relation to fine art. I recently completed my PhD on this subject at Kyoto city University of the Arts, Japan's oldest Art School. Feel free to leave comments or to contact me directly if you'd like any more information on life as an artist in Japan, what a PhD in Fine Art involves, applying for the Japanese Government Monbusho Scholarship program (MEXT), or to talk about diagrams and diagrammatic art in general. Sol Lewitt, Diagram and certificate for wall drawing #49, A Wall Divided Vertically into Fifteen Equal Parts, Each with a Different Line Direction and Colour, and All Combinations, 1970, Ink on paper Towards the end of the 1960s, the American artist Sol LeWitt made a series of groundbreaking works that exist primarily as concepts. These concepts are established by precise sets of diagrammatic instructions that specify which combinations of lines, shapes, colours and dimensions should be used in order to recreate LeWitt's art works in reality. When the diagrammatic instructions are purchased, an accompanying certificate validates the authenticity of the artwork and grants the owner permission to reconstruct the work in a location of their choice. By attributing absolute priority to concept LeWitt gave a Platonic dimension to these artworks, in that he insisted that they exist in essence as ideas in a purely abstract, immaterial way. In the words of LeWitt himself, “the Idea becomes a machine that makes the art.” (1) Radically, LeWitt proposed that in order for an artist to deepen their artistic practice, they should aim to remove their individual subjective decisions and taste from the creative act itself. Again, in the words of LeWitt: "If the artist wishes to explore his idea thoroughly, then arbitrary or chance decisions would be kept to a minimum, while caprice, taste and other whimsies would be eliminated from the making of the art… To work with a plan that is preset is one way of avoiding subjectivity… This eliminates the arbitrary, the capricious, and the subjective as much as possible." (2) Figure 1: Sol LeWitt, “Wall Drawing 85.” June 1971. Colored pencil. LeWitt Collection, Chester, Connecticut. First Installation: LeWitt residence, New York (Art © 2011 The LeWitt Estate /Artists Rights Society, New York) As a young graduate of Medical Biochemistry, the precise and methodical drawings of Sol LeWitt were the first conceptual art works I discovered, and I felt an immediate connection with the process, result and underlying philosophy. Lewitt's stance epitomises what I would now call that of the "Romantic Objective", in that his artistic practice successfully combines the idealistic goals of objectivity with poetic irrationality. (A much more detailed explanation can be found in Chapter 4.1 and 4.2 of my PhD thesis "Romantic Objectivism: Diagrammatic thought in Contemporary Art", which is available for download from the research page of this website.) Looking at the first five propositions from LeWitt’s Sentences on Conceptual Art helps clarify his position, and how he conceives the role that intuition and logic play as devices with in his work: 1. Conceptual artists are mystics rather than rationalists. They leap to conclusions that logic cannot reach. 2. Rational judgements repeat rational judgements. 3. Irrational judgements lead to new experiences. 4. Formal art is essentially rational. 5. Irrational thoughts should be followed absolutely and logically. (3) The diagrammatic format is central to LeWitt's practice and he used diagrams both to store his artistic concepts and then later translate and transcribe them into reality. Imperfections that arise naturally during the process of recreating the works by hand, add a range of tones and textures to the images and, over time, Lewitt found ways to incorporate even this into the nature of the work, as shown in the time lapse video below. The video was made during the installation of his wall drawing #797 at the Blanton museum of Art, in which minor imperfections become amplified due to repetition, adding to the unique character of the final work. Figure 2: Sol Lewitt, Wall Drawing #797 Black, red, yellow, and blue marker on wall Installation view, Feb. 2014 Blanton Museum of Art LeWitt Collection, Chester, Connecticut © 2014 Estate of Sol LeWitt/Artist Rights Society (ARS) Germano Celant discusses this 'noise' added by humans during the process of making / transcribing LeWitt’s work in terms of entropy, a scientific term for measuring the level of disorder within a system: " ...entropy of communication is reduced to the ideal state… in which the visual element is the exact result of a conceptual process [and] permits the extreme purification of the idea or concept, to the point at which it is presented for what it is, a rational and objective entity that does not admit those subjective or empathetic conditions that are part of the usual aesthetic operation. " (4) Celant’s comments are idealistic in terms of the extent to which it is possible to strip an artwork entirely of its subjective nature, and are more suited to the early 'monosemic' works of the French conceptual artist Bener Venet, as we will see in a future post. LeWitt's idealistic goal of objective image making lead him inevitably to the specialised visual language of mathematical geometry in his Location series, in which Platonic-type geometric forms are presented accompanied by labyrinthine poetic-instructional texts. In order for the diagrams of geometry to function, a number of assumptions must first be made so that they can be said to represent the underlying mathematics. For example, a point of ink on paper is taken to represent a conceptual mathematical point of zero dimensions, and an ink line is understood as representing a perfect one-dimensional line of zero width. Such paradoxical ambiguities are simply overlooked during the reading of such images, and the American Philosopher and Semiologist Charles Sanders Peirce referred to such inconvenient physical qualities as "accidental characters that have no significance”. (5) Figure 3: Sol LeWitt, Location of a circle, from the series: The location of six geometric figures (circle, square, triangle, rectangle, parallelogram and trapezoid). 1974, Set of six etchings, Edition of 25 10 AP. Sol LeWitt uses the high-fidelity, low-entropy notation of geometry, but contrasts it with a convoluted textual description of, or instructions for, each of his six geometric diagrams. He also chose to write the texts using everyday language rather than the efficient and specialised symbols of mathematics, and the result is a single sentence, hundreds of words long and almost impossible to mentally reconstruct. Figure 4: Sol LeWitt, The location of six geometric figures (circle, square, triangle, rectangle, parallelogram and trapezoid). 1974, Set of six etchings, Edition of 25 10 AP. The texts accompanying each geometric image become almost religious mantras, where meaning is lost within the sounds of the words themselves. This fascinating juxtaposition of text and pure notation results in a poetic resonance that is "Romantic-Objective" as well as diagrammatic in nature: Location of a Circle: A circle whose radius is equal to half the distance between two points, the first point is found where two lines would cross if the first line were drawn from a point halfway between a point halfway between the center of the square and the upper right corner and the midpoint of the topside to a point halfway between a point halfway between the center of the square and the midpoint of the right side and a point halfway between the midpoint of the right side and the lower right corner, the second line of the first set is drawn from a point halfway between a point halfway between the center of the square and a point halfway between the midpoint and the left side and the upper left corner and the midpoint of the left side to a point halfway between a point halfway between the center of the square and the upper right corner and a point halfway between the midpoint of the right side and the upper right corner; the second point is found where two lines would cross if the first line is drawn from a point halfway between a point halfway between the center of the square and the midpoint of the bottom side and a point halfway between the center of the square and the lower left corner to a point halfway between the end of the first line of the first set and the end of the second line of the first set, the second line of the second set is drawn from a point halfway between the point where the first two lines have crossed and a point halfway between the start of the first line of the first set and a point halfway between the midpoint of the left side and the upper left corner to a point halfway between the end of the first line of the second set and the midpoint of the bottom side; all whose center is located equidistant to three points, the first of which is located at the center of the square, the second point is located at a point halfway between a point halfway between the center of the square and the upper left corner, the third point is located halfway between the start of the first line of the first set and the end of the first line of the second set. Nicholas Baume describes the location of six geometric figures (also produced as wall drawings) as one of LeWitt’s most disciplined and exacting works, and yet also his most absurd and wryly funny, suggesting that the text is a “form of abstract verbal play” for LeWitt. (6) Importantly, LeWitt himself once remarked that he considered his Location series his “poetry”. (7) It is worth noting at this point that a strikingly similar example of pure geometric notation juxtaposed with its dense description in text can be found over half a century earlier the notebooks of Leonardo da Vinci, circa 1448 : Figure 6: Leonardo da Vinci, Profile of a Man, plant, geometric figures etc. (also known as the ‘Theme Sheet’) (detail) c. 1448, pen and ink, Windsor Castle, The Royal Collection. Accompanying text: ( Located in the bottom left hand corner of image above ) " The triangle abc is similar to a third of the large triangle dbf because it is made up of two equal parts, that is abe and bec, and the large triangle is made up of 6 parts, and each of these parts is equal to each of the said 2, and the 6 parts are these: dec and ced and so on, in similar parts. And if the triangle abc had its sides similar to its axis, cb, the triangle dbf would receive in itself 4 of these triangles, whereas at present it receives 3; thus to see the difference from one of the triangles which are ¼ of the large one and one of those which are ⅓, have the large triangle divided in to twelfths, and say that it is 12 twelfths. Then say that the triangle which is a ⅓ of it is 4 of these twelfths and the triangle that is a ¼ of this large one contains three of these twelfths, so that the difference between 4 and 3 is one twelfth, whence we can say that the smaller is ¾ of the larger. " The following selection of geometry diagrams are taken from the beautifully designed German book "der Geometrie descriptive" c.1865, by Leopold Mossbrugger. Fig.a in image 3, presents the various line types employed during the construction of these ideal types of mathematical forms, and the diagrammatic systems used to bring them into being as two dimensional lithographs upon the page. This particular copy was purchased from an antiquarian bookstore in Prague, the capital the Czech Republic, in 2002 . Figures 7-27: Selected images from "der Geometrie descriptive" by Leopold Mossbrugger, c.1865 References: 1) LeWitt, S. (1967) Paragraphs on Conceptual Art. Art Forum. June, 1967 2) Ibid 3) LeWitt, S. (1969) Sentences on Conceptual Art. In: Art and Language, No. 11. (May 1969) p. 11 4) Celant, G. (2009) (First published:1988) The Sol LeWitt Orchestra. In: Sol LeWitt: 100 views. Eds. Markonish, D. and Cross, S. MASS MoCa in association with Harvard University Press, p. 27. 5) de Waal, C. (2013 ) Peirce: A guide for the perplexed, London: Bloomsbury Academic. p.88. 6) Baume, N. (2001) Sol LeWitt: Open cubes. Exhibition Catalogue. Hartford: Atheneum Museum of Art. 7) Lewitt, S. quoted in: LeWitt and Miller Keller, A. Excerpts from a Correspondence, 1981 – 1983. In: Suzanne Singer, ed., Sol LeWitt wall drawings, 1968 – 1984. Amsterdam: Stedelijk Museum, Eindhoven: Van Abbemuseum, Hartford: Wadford Atheneum, 1984. p. 18-25.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Dr. Michael WhittleBritish artist and Posts:
Categories
All
Archives
April 2024
|