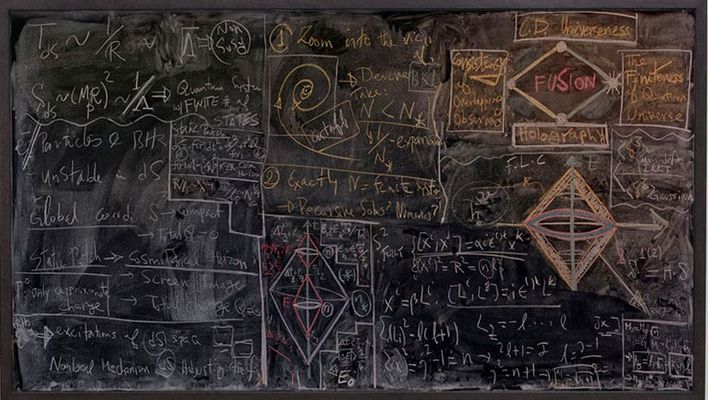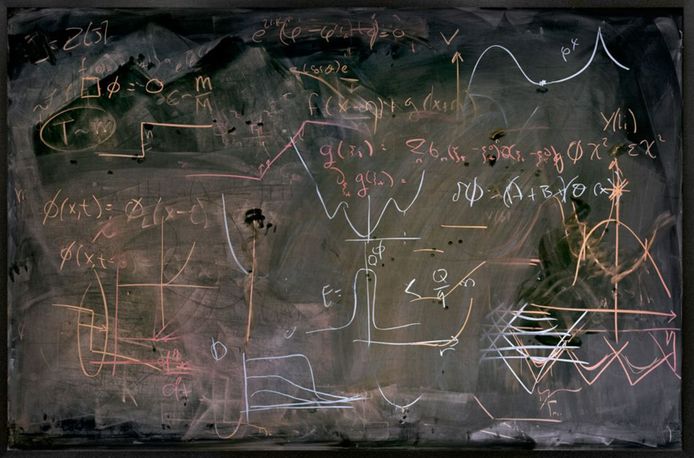|
❉ Blog post 14 on diagrams in the arts and sciences considers the role of diagrams in theoretical and particle physics, as powerful conceptual tools to gain unexpected insights in to the fundamental nature of reality. Figure 1: Lecture scene from the Coen Brother's Academy Award winning file 'A serious Man', 2009. The previous blog looked at some of the difficulties involved in diagramming ideal geometric forms in mathematics, and how the natural limits to human vision affects the accuracy of their interpretation. Despite such shortcomings, diagrams still play an extraordinary variety of roles at the frontiers of mathematical knowledge production, where they help fathom some of the most complex patterns the human minds is capable of comprehending. Mathematician, astronomer and physicist C.F. Gauss famously asserted that: "Mathematics is the Queen of the Sciences, and Arithmetic the Queen of Mathematics. She often condescends to render service to Astronomy and other natural sciences, but under all circumstances the first place is her due." (1) This notion of mathematics in service to science is most discernible in the intimate relationship between maths and physics. In the introduction to Eric Temple Bell's book 'Mathematics - Queen and Servant of Science', titled in reference to Gauss, we're reminded how important advances in pure mathematics have sometimes found application many years after the initial discoveries were made. Without the non-Euclidean Geometry that Riemann developed in 1854, for example, Einstein would have been unable to state his theory of General Relativity and Gravitation in 1916. While mathematics may still retains a position of sovereignty within contemporary science, the relationship is no longer so one sided. Research in contemporary physics has developed such a rich and sophisticated mathematical language of its own that it's quite capable of inspiring insights within the field of mathematics itself. The sheer complexity of the calculations involved in string theory for example, lead physics titan Edward Witten to describe them as a bit of 21st century physics that somehow dropped into the 20th century. Witten's own work in string theory was revolutionary and led Witten to mathematical results so profound that he become the first physicist to be awarded the Fields medal for mathematics in 1990. With this in mind, this blog entry considers some of the most profound, mysterious and powerful diagram in physics, diagrams which seem to transcend their mathematical origins and function at meta-levels in terms of their efficiency and the value of their insights. The first and most iconic example of such diagrams is the Feynman diagram, named after the American physicist Richard Feynman (1918-88). Feynman was the eccentric 'genius's genius' with a legendary reputation for creative problem solving and the ability to teach the complexities of quantum physics to students and non-physicists.
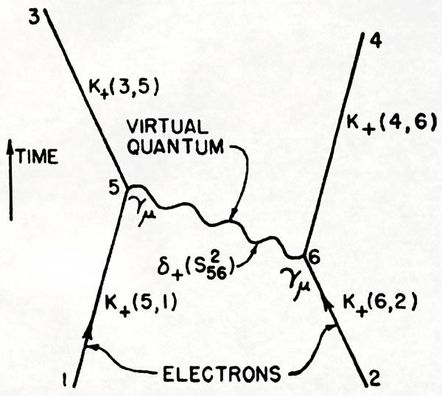
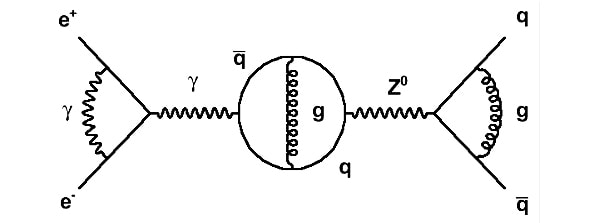
The points where one line connects to another is known as a vertex, and this is where the particles meet and interact: by emitting or absorbing new particles, deflecting one another, or changing type. The Feynman diagram in figure 2 sketches out a map of the mathematical expression: e 2 ∫∫d4 x5 d4 x6 K+(3,5)K+(4,6)γµδ+(s 56 2 )γµK+(5,1)K+(6,2). In it's simplest interpretation two electrons interact, trade a virtual photon and then scatter as a result of their interaction. Figure 3: Richard Feynman with his family in front of his 1974 Dodge Tradesman van, which he decorated with hand painted Feynman diagrams. The visual clarity and precision of feynman diagrams belies the quantum uncertainty of the subatomic collisions and scatterings events they depict. Unlike a bubble chamber image, only the sum of all the Feynman diagrams represent any given particle interaction; particles do not opt for a one diagram or another each time they interact. At the quantum level particles interact in every way available to them, and so an exact description of the scattering process involves summing up a large number of diagrams, each with their own mathematical formula for the likelihood they will occur. In this way a single Feynman diagram represents all possibilities of an interaction from its initial to final state, and so the connections of a Feynman diagram are more important than the configuration of it's lines, squiggles, loops and dashes. Pioneer of data visualization and expert on information graphics Edward Tufte, had 120 Feynman diagrams constructed in stainless steel (see figure 4). His wall mounted constructs represent all 120 different ways that a 6-photon scattering event can be depicted. Figure 4: All possible 6-photon scattering (120 space-time Feynman diagrams), 2012, Edward Tufte, Wall mounted installation of stainless steel with shadows, 530 x 230 x 10 cm (Installation view at Fermilab) Feynman introduced his ingenious schematic in 1948, but by the 1980's their limitations were starting to become apparent, and Feynman himself went on to prove that the diagrams were only approximations that involved an enormous amount of redundancy that arose from their reliance on involving virtual particles (see figure 2). Feynman diagrams were designed to describe all the possible results of subatomic particle collisions, but even a seemingly simple event like two gluons colliding to produce four less energetic gluons, involves some 220 diagrams. Such collisions occur billions of times a second during experiments carried out using modern day particle accelerators. In the mid-2000s patterns began to emerge from events recorded in particle accelerators that repeatedly hinted at an unknown, underlying, coherent mathematical structure. A new set of formulas were proposed by the physicists Ruth Britto, Freddy Cachazo, Bo Feng and Edward Witten, known as the BCFW recursion relations after their discoverers. The formulas dispense with familiar variables of Feynman diagrams such as position and time, and involves an entirely new diagrammatic system first developed in the 1970's by Roger Penrose, named twistor diagrams.
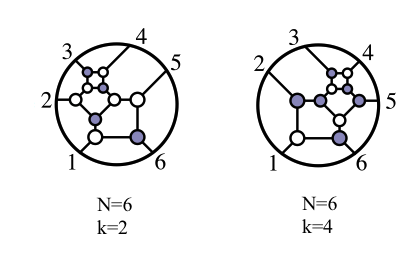
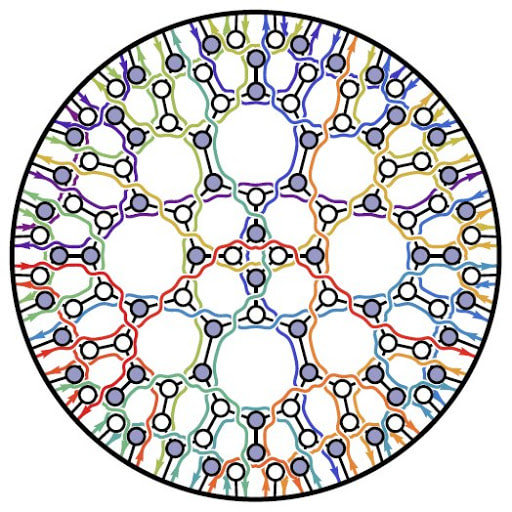
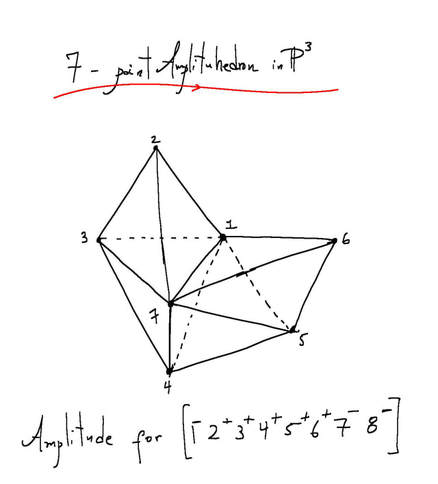
The incredible simplicity and power of twistor diagrams gave them an air of mystery according to Arkani-Hamed: “The terms in these BCFW relations were coming from a different world, and we wanted to understand what that world was.” (3) After over a decade of research with his collaborators, Arkani-Hamed showed how twistor diagrams could be pieced together to create a timeless, multidimensional object known as an 'Amplituhedron' (figure 6). Figure 6: 'On-shell diagrams' are a new visual system for guiding and structuring the calculations of what happens when physical 'on-shell' particles interact, as opposed to the 'off-shell' virtual particles of Feynman diagrams. The Amplituhedron has been described as an intricate, multi-faceted, higher dimensional jewel at the heart of quantum mechanics, a meta-level Feynman diagram completely new to mathematics.
From Feynman diagrams to twistor diagrams and the discovery of the enigmatic amplituhedron, diagrams remain a powerful, albeit mysterious tool in theoretical physics. They permit information to be stored and shared with high fidelity, but they also mobilise and shape new knowledge by allowing intuition and rational thought to play a role in the creative process. Diagrams in actions - the photography of Alejandro Guijarro Alejandro Guijarro, STANFORD III, 2012, C-type print, 117 x 240 cm For his 'Momentum' series (2010-2013), Spanish photographer Alejandro Guijarro traveled to several international academic institutions that specialize in quantum mechanics: CERN, Stanford, Berkeley and Oxford. In a form of documentation, Guijarro measured and photographed blackboards that he found in lecture theatres, meeting rooms and offices, then printed the images at a 1:1 scale. The series highlights the transitive nature of diagrams at work during the creation and transmission of knowledge. It presents the process as a physically involved gestural performance, as various trains of thought are followed and erased to leave a blurred palimpsest. 'Momentum' is reminiscent of Marcel Duchamp’s project 'Unhappy Readymade', discussed in this previous Blog: The Diagrams of Geometry part II- A soggy book of diagrams as a wedding present from Marcel Duchamp. Both projects present us with a token of something lost - information and knowledge made manifest through the substrates ink, paper, chalk and board only to be subject to entropy. In the case of 'Unhappy Readymade' it's the wind and rain which add entropy, in the case of Guijarro’s 'Momentum' it's the hand of the professor, janitor or the student armed with a blackboard eraser that return the arena of ideas to a tabula rasa. Alejandro Guijarro, BERKLEY II, 2012, C-type print, 112 x 236 cm Alejandro Guijarro, CAMBRIDGE VII, 2011, C-type print, 120 x 300 cm Alejandro Guijarro, BERKELEY VIII, 2011, C-type print, 117 x 174 cm Alejandro Guijarro, SLAC V, 2012, C-type print, 117 x 180 cm Alejandro Guijarro, SLAC V, 2012, C-type print, 117 x 180 cm Alejandro Guijarro, OXFORD I, 2011, C-type print, 110 x 150 cm Notes:
1) C.F. Gauss quoted in Gauss zum Gedächtniss (1856) by Wolfgang Sartorius von Waltershausen 2) Andrew Hodges, Online at: http://www.twistordiagrams.org.uk/papers/ 3) Arkani-Hamed, quoted in 'A Jewel at the Heart of Quantum Mechanics' by Natalie Wolchova, online at: https://www.quantamagazine.org/physicists-discover-geometry-underlying-particle-physics-20130917/ 4) Jacob Bourjaily, quoted in 'A Jewel at the Heart of Quantum Mechanics' by Natalie Wolchova, online at: https://www.quantamagazine.org/physicists-discover-geometry-underlying-particle-physics-20130917/
0 Comments
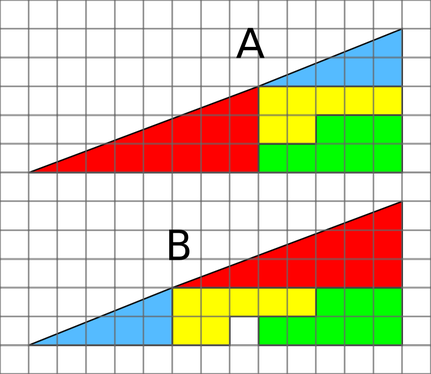
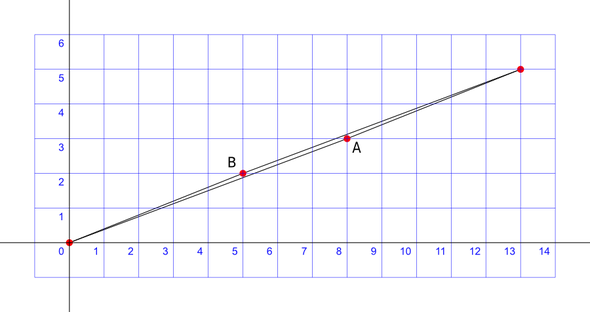
❉ Blog post 13 on diagrams in the arts and sciences explores Mathematic's love/hate relationship with diagrams, and May Ray's favourite 'Shakespearean equations'. Max Ernst, 'Spies', Plate 10, cover illustration for Paul Eluard's book of poetry 'Repetitions', published 1922 " A mathematician, however great, without the help of a good drawing, is not only half a mathematician, but also a man without eyes. " Lodovico Cigoli to Galileo Galilei, 1611 Diagrams hold an important but controversial position in Mathematics, particularly within the field of geometry, where they are primarily regarded as a method of enhancing comprehension of a proof rather than partaking in rigorous mathematical reasoning. A number of simple, cautionary examples of the problematic relationship between Maths and diagrams exist as diagrammatic puzzles, and a famous example is the 'Missing Square Puzzle' shown in figure 1.
The natural limits to the acuity of human vision affects the way that we make estimations about the shapes of triangle A and B, and whether or not their lines are straight. The diagram in Figure 2 reveals that objects A and B are actually 4-sided quadrangles, rather than triangles. Neither of their hypotenuse (the longest side of the triangle ) of are straight lines. Figure 2: Graph of two false Hypotenuse for triangle A and B, neither of which are truly straight. If we return to look again at figure 1, the small difference in the angle of slope of the blue and red components is indistinguishable, especially when spread across a distance. However in reality, their difference totals one unit of area, and this explains the seemingly miraculous origins of the missing square. Marcel Duchamp was fascinated by the idea of a parallel world of Mathematical perfection that exists alongside the chaos and imperfection of reality and daily experience. This was the subject of the blog post: 'A soggy book of diagrams as a wedding present from Marcel Duchamp', which considered one of Duchamp's less well known projects using a found book of Euclid's Geometry.
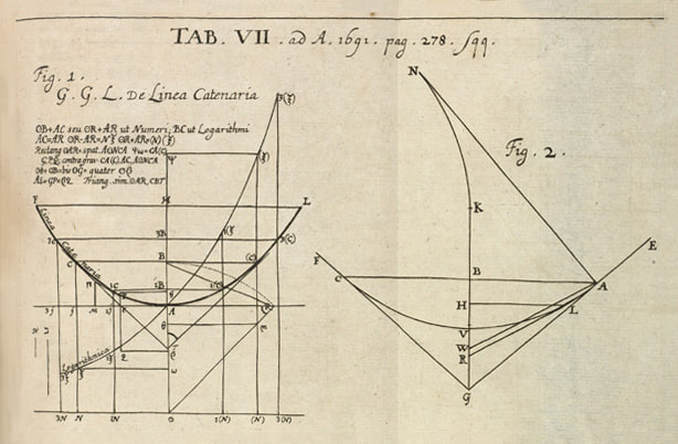
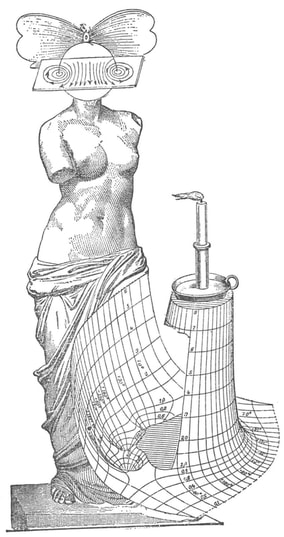
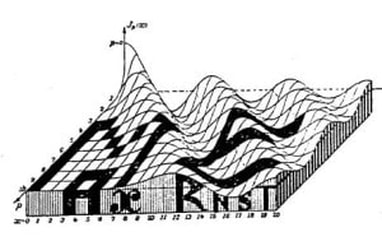
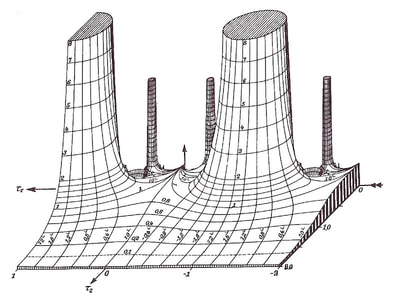
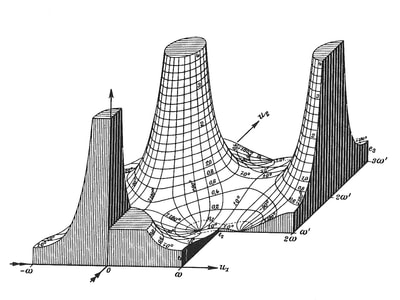
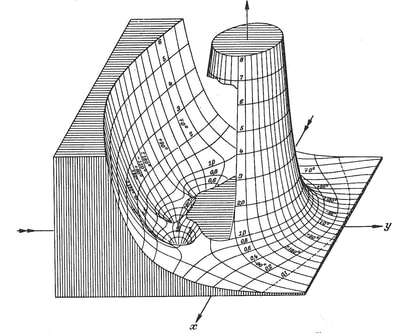
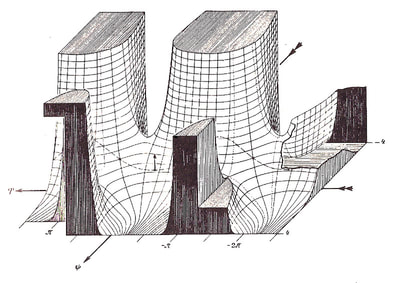
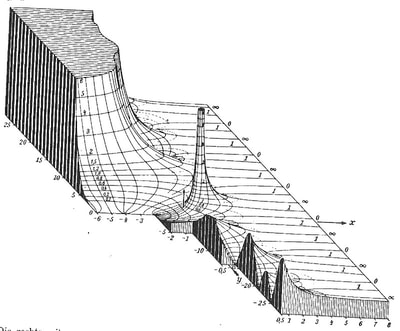
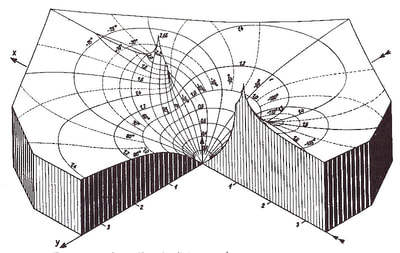
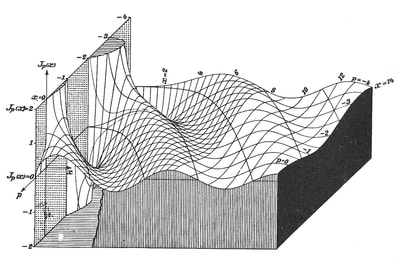
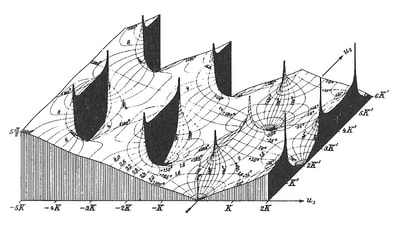
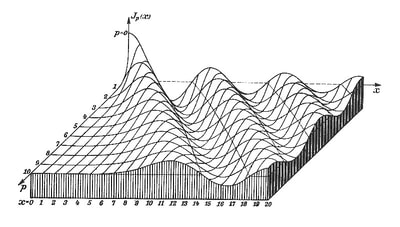
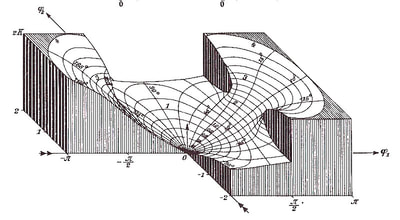
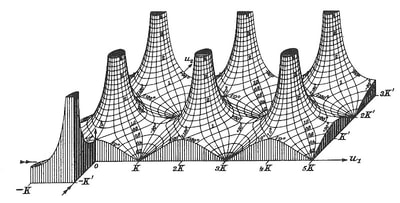
The quote I used to introduce this blog is taken from a letter written by the Italian artist Lodovico Cigoli to his lifelong friend the scientist Galileo Galilei. (1) Both men shared a passion for art and science. Galileo's interest in art is the subject of an extensive study by Erwin Panofsky, in his 1954 book 'Galileo as a Critic of the Arts'. Cigoli was interested in mathematics, science, geometry, and wrote an extensive treatise on perspective. For Lodovico Cigoli, a good 17th century diagram provided a visual means of gaining a deeper insight into the mathematics of nature. However, over the course of the following two centuries, the role of the diagram shifted to the extent that it became considered more of a veil that obscured the essence of mathematics, and algebra was proposed as the only way to lift the veil. Writing in the early 18th century, in a statement that anticipates the predominate modern view, the philosopher and mathematician Leibniz asserted that: "...it is not the figures which furnish the proof with geometers, though the style of the exposition may make you think so. The force of the demonstration is independent of the figure drawn, which is drawn only to facilitate the knowledge of our meaning, and to fix the attention; it is the universal propositions, i.e., the definitions, axioms, and theorems already demonstrated, which make the reasoning, and which would sustain it though the figure were not there." (2) Figure 4: Diagrams submitted to accompany solutions describing the shape of a Catenary curve, by Gottfried Leibniz (Figure 1 left) and Christiaan Huygens (figure 2 right) to Jacob Bernoulli for publication in the Acta Eruditorum, 1691 It's important to bear in mind our visual limitations and the way our brain makes approximations when reading the diagrams of mathematics. This and the fact that real-world diagrams of perfect mathematical objects ultimately rely upon imperfect lines of ink, chalk or pixels. However, the diagram remains an extremely powerful tool and a visual guide in providing an insight into the austere and pristine world mathematical geometry and topology. Leibniz's own notebooks contain an astounding array of diagrammatic sketches that accompany his mathematics, as in figure 4, and the designs and calculations for his 'Universal Calculator', some 200 years before the work of Charles Babbage. For an interesting introduction to the notebooks of Leibniz, see Stephen Wolfram's blog: Dropping In on Gottfried Leibniz. For centuries mathematicians have constructed 3D diagrammatic models to illustrate mathematical concepts to students. A famous collection of these models is housed at the Institut Henri Poincaré in Paris. Between 1934 and 36, the American artist Man Ray made several visits to the Institut to photograph the collection, accompanied by Max Ernst. The Greek art critic and publisher Christian Zervos used the photographs for an article in the Parisian Cashiers d'art, and the images quickly became famous in Surrealist circles. Man Ray described the models that he found languishing in dusty cabinets as 'so unusual, as revolutionary as anything that is being done today in painting or in sculpture', though he admitted that he understood nothing of their mathematical nature. When the Second World War came to Paris in 1940, Man Ray relocated to Hollywood, where he started work on a series of 'suggestively erotic paintings' based on his 1930's photographs. Under the title of the 'Shakespearean Equations', he later referred to the paintings as one of the pinnacles of his creative vision. Below are images of selected paintings from the 'Shakespearean Equations' series, Juxtaposed alongside the original mathematical models they were based upon. Note: An extensive online collection of mathematical models is available here: the Schilling Catalogue of Mathematical models Figure 5: Selection of paintings from Man Ray's 1940's 'Shakespearean Equations' series, shown alongside the models they were based on, from the Institut Henri Poincaré, Paris. An important and influential book on Mathematical diagrams was Eugene Jahnke and Fritz Emde’s 'Funktionentafeln Mit Formeln und Kurven' (Tables of functions with formulae and curves). This landmark publication on complex mathematical surfaces and functions was first published in 1909, and a selection of graphs taken from the 1933 edition of the book are shown below, courtesy of Andrew Witt. As Witt points out in his own blog on this series here: Functional Surfaces I, it's said that the architect Le Corbusier kept a copy in his studio whilst designing the Phillips Pavilion. Max Ernst appropriated from the book for a series of collages and poems in the catalogue accompanying his 1949 exhibition 'Paramyths'.
Figure 8: A selection of diagrams from the 1933 edition of 'Funktionentafeln Mit Formeln und Kurven', by Eugene Jahnke and Fritz Emde, courtesy of Andrew Witt. AFTERWORD:
Jos Leys, Dodecahedral Tessellation of the Hypersphere: a dissection of the 120-cell in 12 rings of 10 dodecahedrons References:
1) Some 29 letters from Cigoli to Galileo remain, however only 2 letters from the scientist to the painter are left, as the artist's heirs chose to destroy all incriminating evidence of their association, after the papal condemnation of Galileo. (In 1610 Cigoli received from Pope Paul V the assignment to paint the dome of Santa Maggiore Maggiore with the Immaculate Conception, the Apostles and Saints.) 2) Leibniz1704, New Essays: 403 |
Dr. Michael WhittleBritish artist and Posts:
Categories
All
Archives
April 2024
|