|
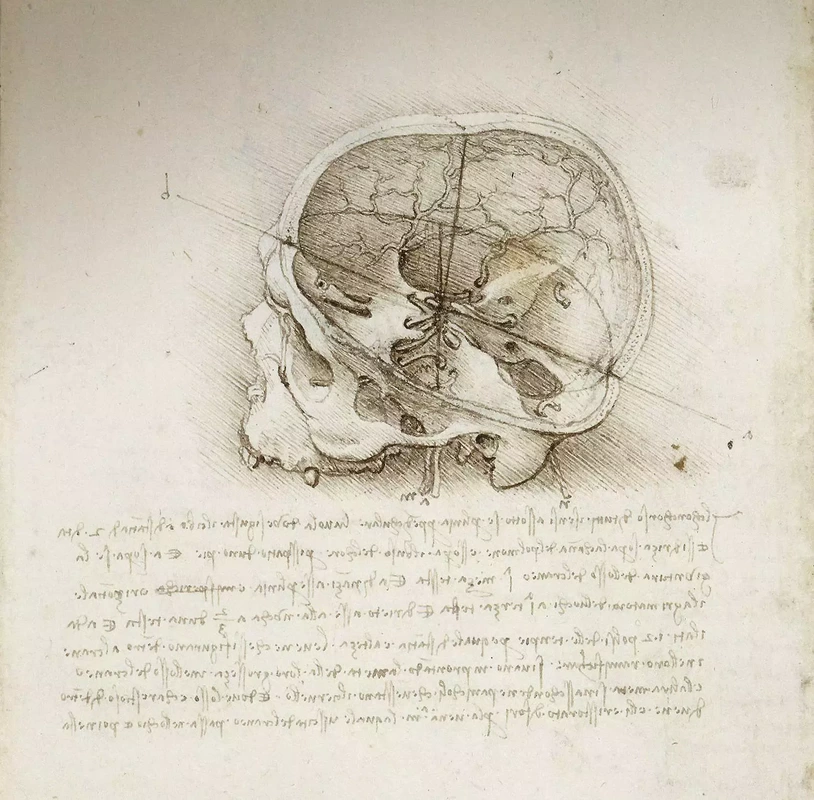
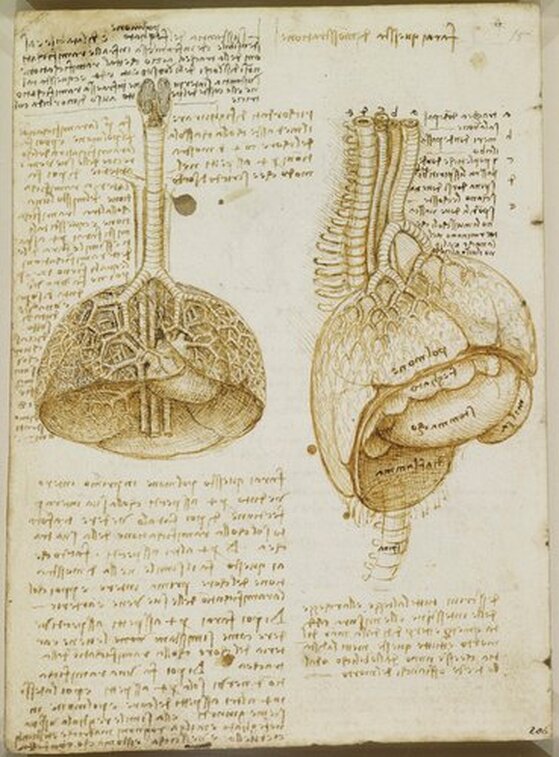
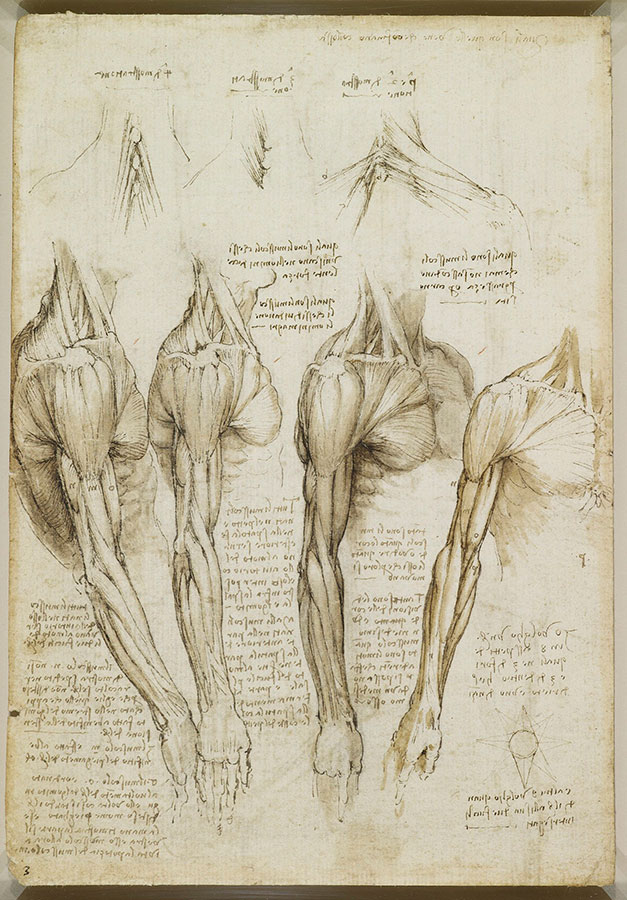
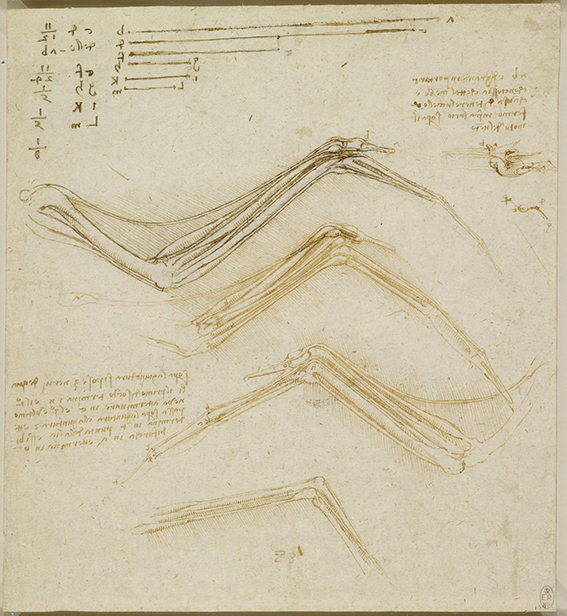
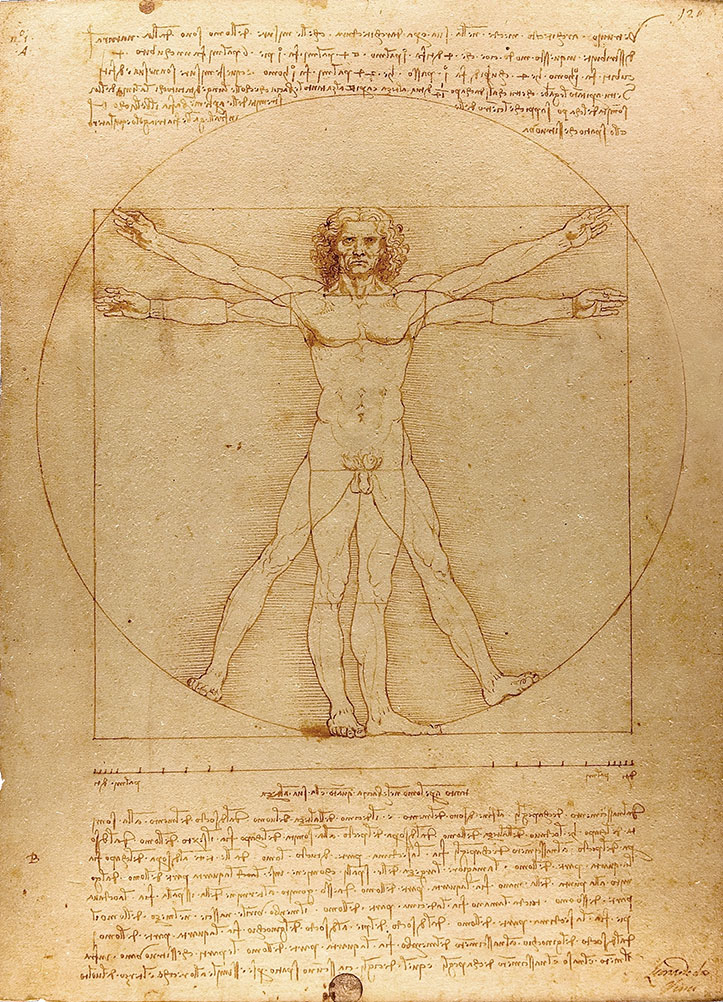
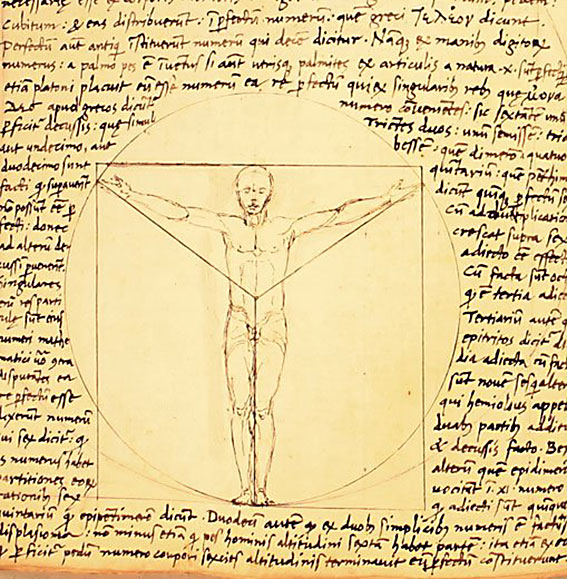
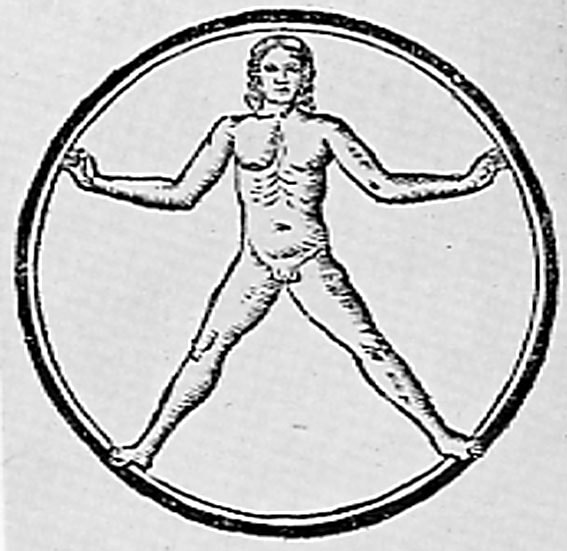
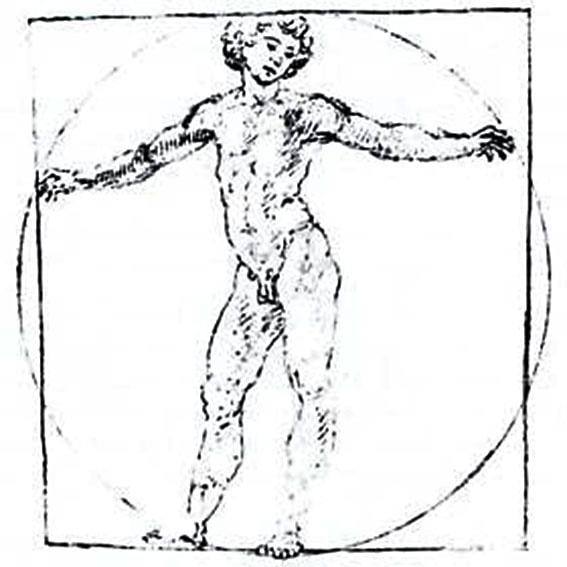
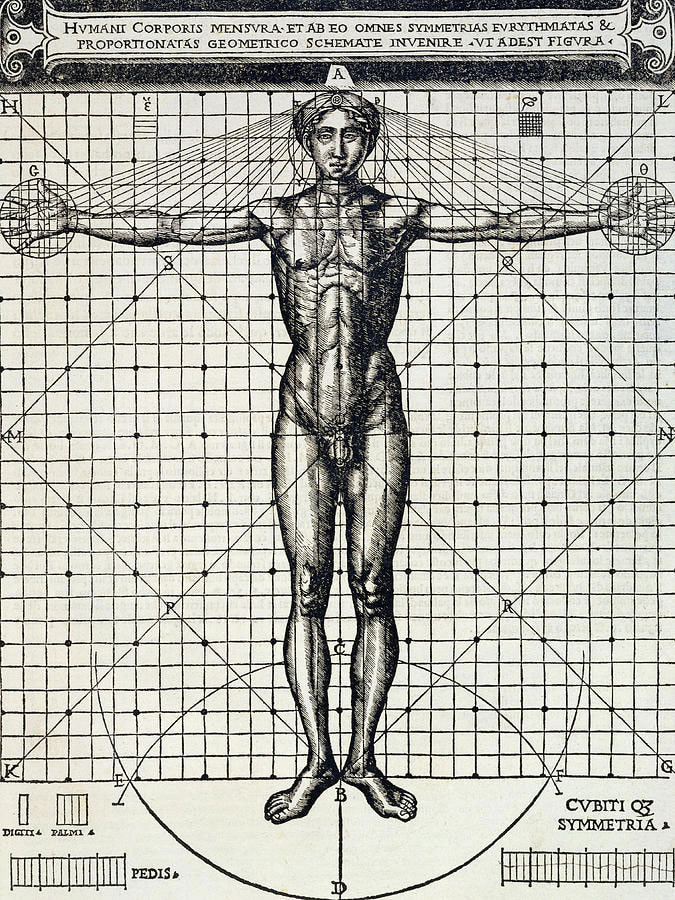
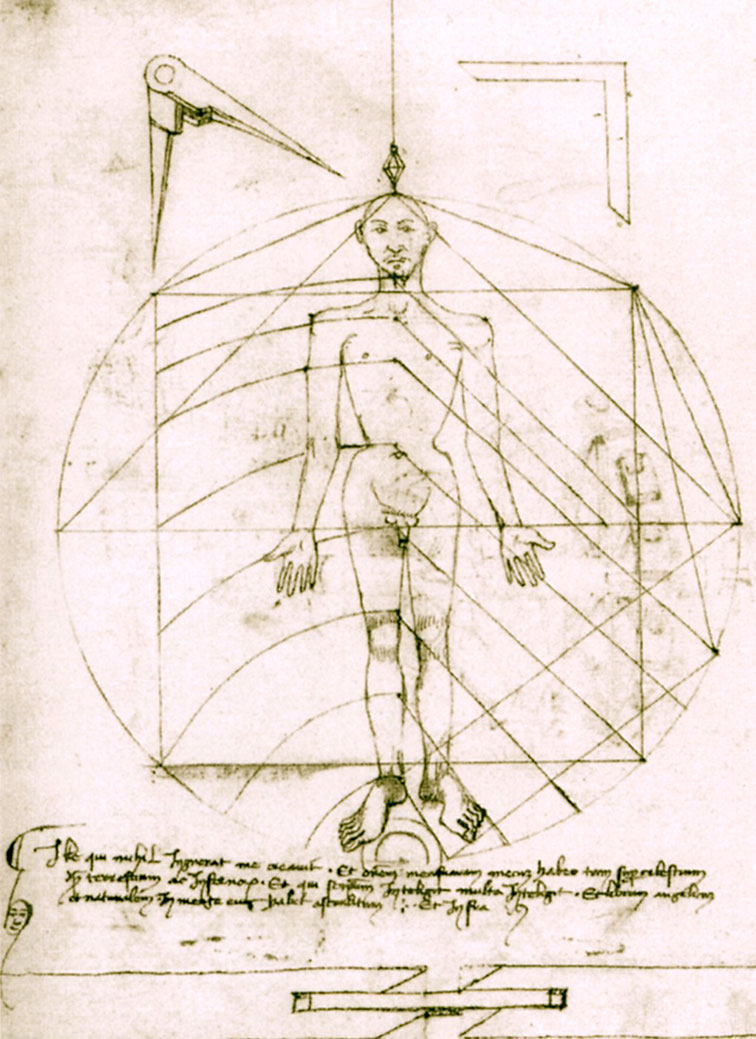
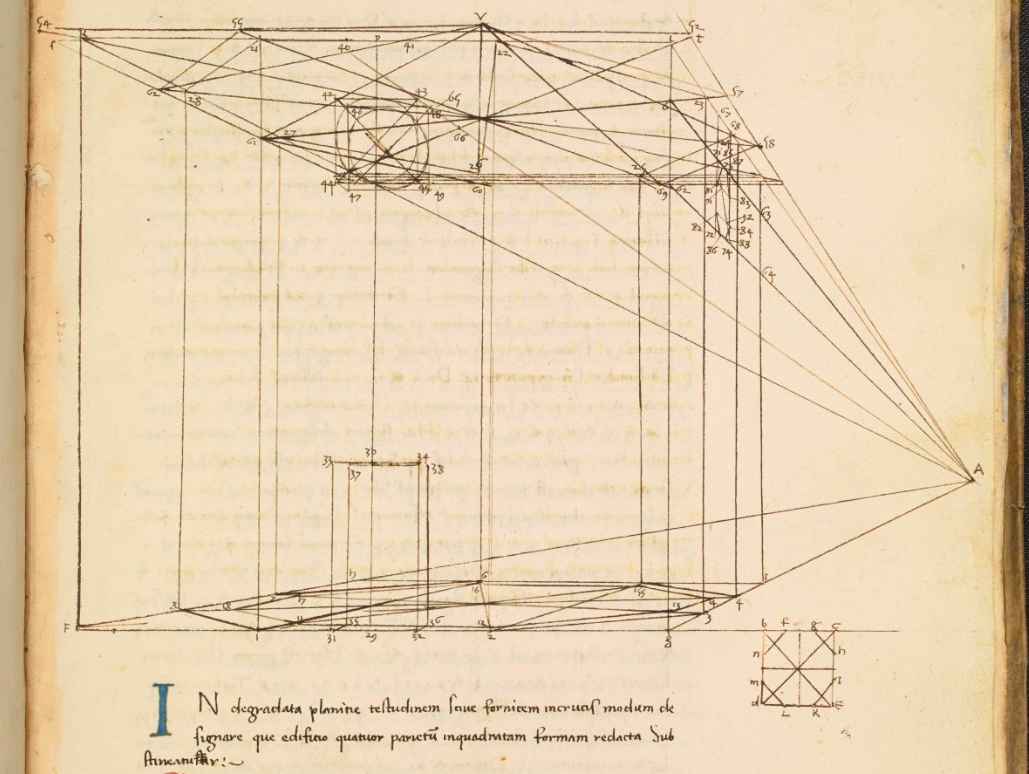
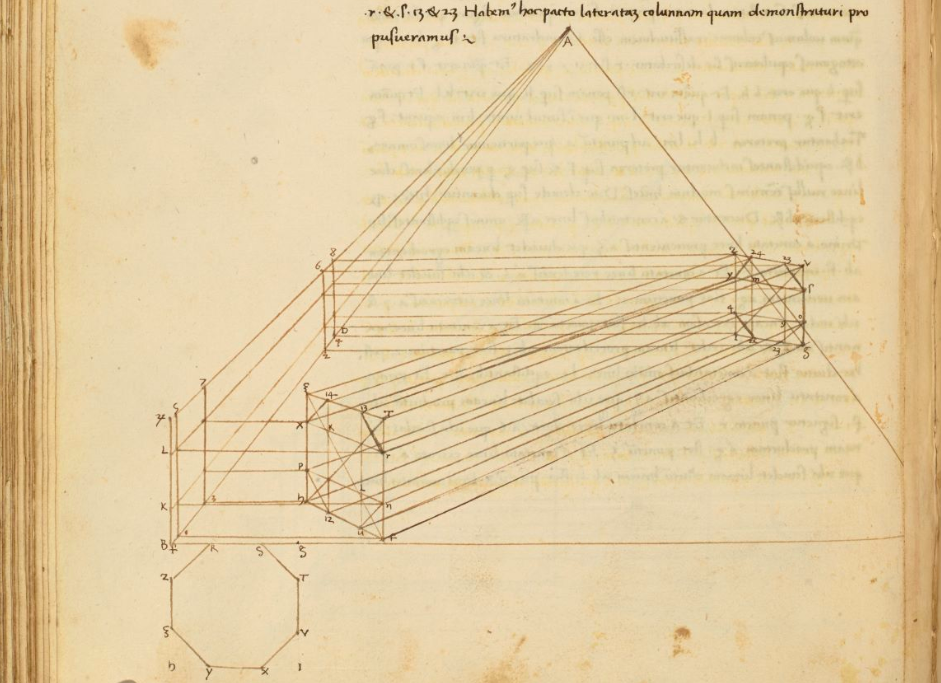
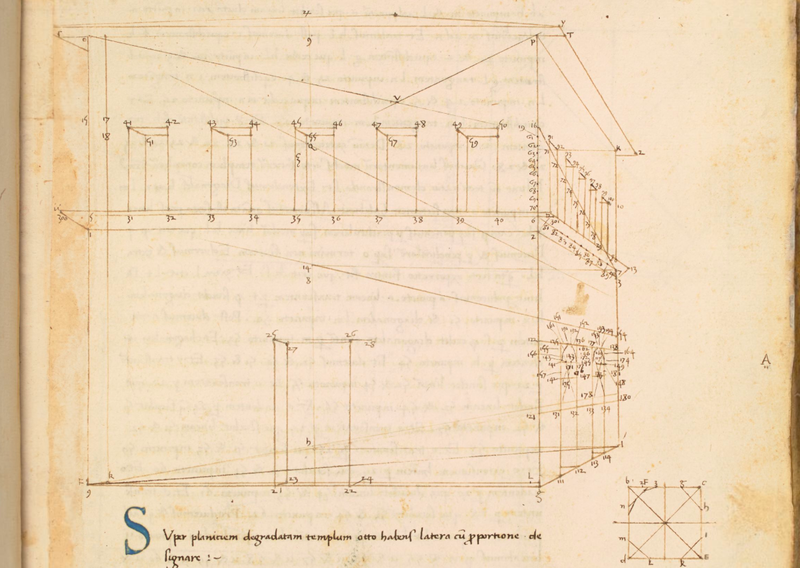
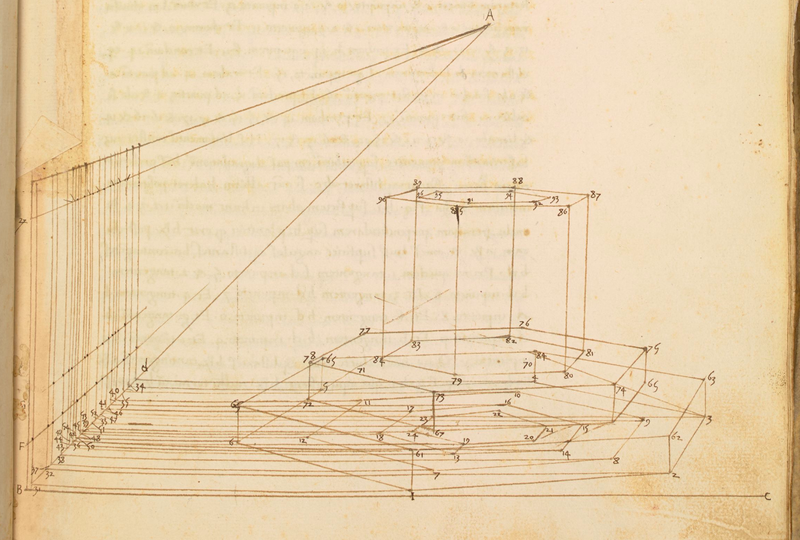
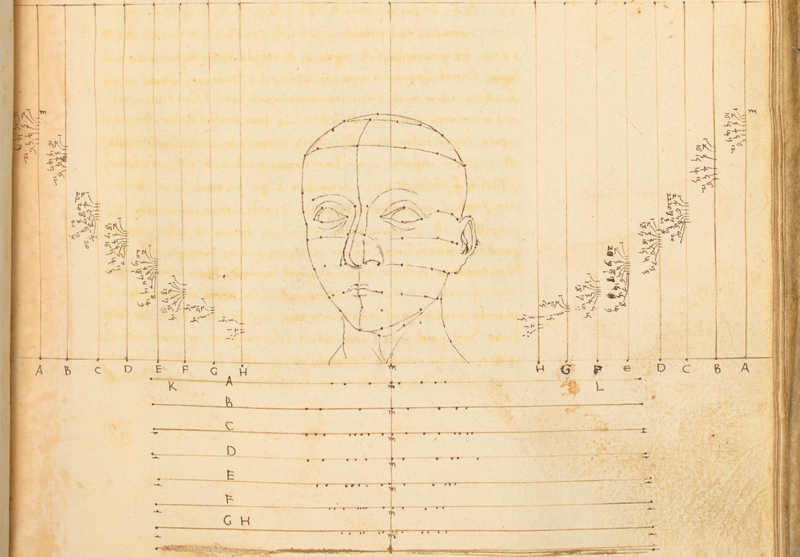
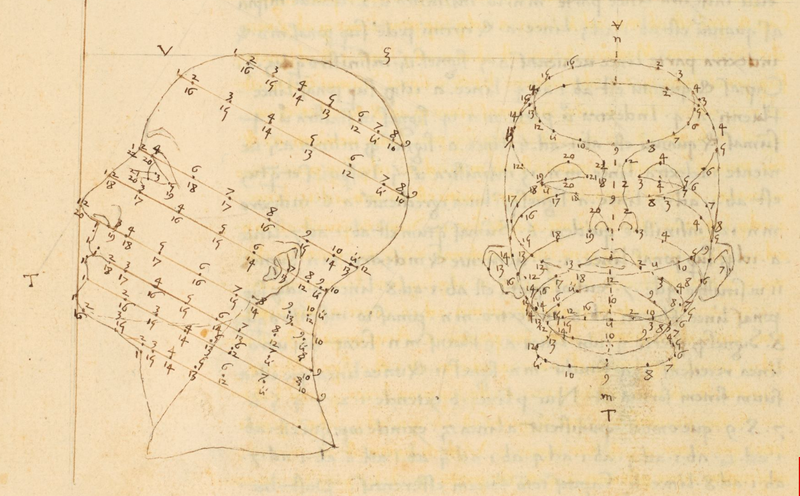
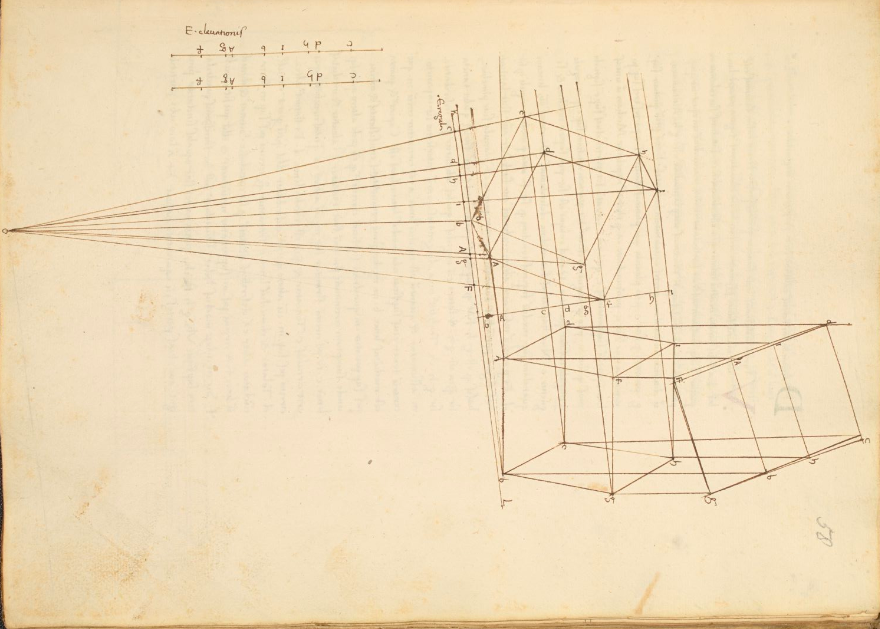
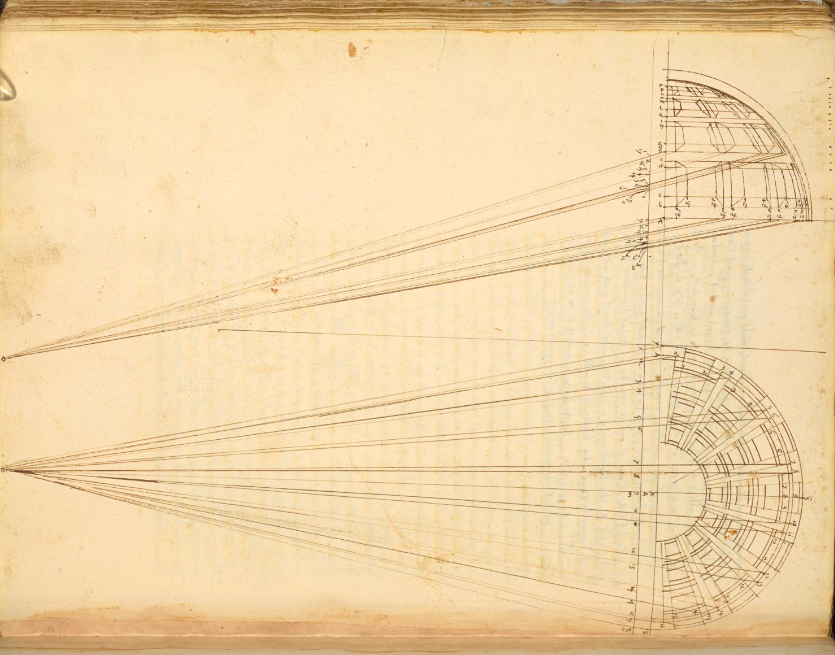
❉ Blog post 20 on diagrams in the arts and sciences delves in to Leonardo Da Vinci's life long obsession with diagram making. From documenting ideas and observations, to elaborate mechanical instructions, blueprints for buildings and sketches for paintings, the diagram was the creative engine that drove his endless pursuit of knowledge and understanding. 1) Glimpse into the left side of a human skull, about 1651 © Royal Collection Trust / Her Majesty Queen Elizabeth II (CC BY-NC-SA 4.0) The surviving notebooks of early Renaissance artist and polymath Leonardo da Vinci (1452-1519) reveal a masterful fluency in his use of diagrams. Indeed, during certain periods, his distinctive mirror-written notes and diagrammatic sketches were his medium of choice for observing and analysing the world, rather than drawing and painting. However as we'll see, all of these modes of exploration and expression were intimately connected, especially so in the case of his complex preparatory diagrams that underlie some of his major paintings. Geometry was fundamental to Leonardo’s process of understanding both the visible forms of nature and the hidden mechanisms and forces underlying natural phenomena. His vision of the interplay of these rules of geometry was transformative and dynamic rather than static, as if he observed nature as a process of geometry in action. He was however not merely content to record how something worked, but also strove to find out why it worked the way it did, and it was this insatiable curiosity that transformed a technician into a scientist. (1) In the words of the great da Vinci scholar Martin Kemp, for Leonardo, the "...muscles of the human body worked immaculately according to the laws that governed levers. The flow of the blood in the vessels and of the air in the bronchial tubes in the lungs was governed by the geometrical rules that applied to all branching systems. A flying bird was designed in perfect conformity with the geometry of airflow.” (2) (See figures 2-5) Leonardo studied anatomy and the proportions of the human body throughout his career, and applied this deep understanding in drawings such as The Vitruvian Man (c.1490) (figure 6). This diagrammatic sketch was Leonardo's attempt to answer an ancient puzzle set 1500 before his time by the first century Roman architect and engineer Marcus Vitruvius Pollio (c. 75–25 BCE). In his book De Architectura, Vitruvius founds his theory of architecture on the proportions of the human body, which he considered nature’s greatest work. The challenge was to show how the human figure can be positioned within a circle and a square with the navel at the centre. Ancient thinkers had long invested the circle and the square with symbolic powers, with the circle representing the cosmic and the divine, and the square the earthly and the secular. Leonardo's elegant solution was to position his figure so that the navel aligned with the centre of the circle, but then to position the square off-centre in alignment with the base of the circle. (figure 6) 6) The Vitruvian Man, c. 1490 Pen and ink with wash over metalpoint on paper, 34.6 cm × 25.5 cm Interestingly, a number of other artists from around the same period also attempted solutions to the Vitruvian puzzle, and some comparative examples are included below that highlight the refined technical elegance of Leonardo's draftsmanship and his exceptional knowledge of anatomy. One drawing in particular, made by Leonardo's close friend Giacomo Andrea Da Ferrara, actually predates that of Leonardo's, and its rediscovery in a lost manuscript in Ferrara, Italy in 1986, lead some art historians to question whether or not Leonardo's drawing was actually of copy of his friend's solution. (3) (See figure 9) 7) Perspective study for the adoration of the Magi, c. 1481 Ink on paper, 16.3 x 29 cm, Florence, Galleria degli Uffizi Leonardo’s preparatory study for the adoration of the Magi is one of his most remarkable sketches. (figure 7) The immaculately depicted geometry of the tiled floor and the static architecture of the temple interior highlight the turbulent graphic images of the figures and animals depicted within it. British art historian Kenneth Clark described the drawing as "a carefully measured courtyard invaded by a retinue of ghosts". Clark considered it one of Leonardo's most revealing drawings, and the earliest evidence of his scientific attainments in perspective, which to his mind provided "a scaffold for the artist's imagination." (4) Likewise, Martin Kemp considers the sketch an exemplar of the paradoxical combination of contained measure and unconstrained improvisation characteristic of many of Leonardo’s drawings. (5) The reduction of complex natural forms to their underlying geometrical relations was, however, more of an intuitive process for Leonardo than one relying upon the techniques of mathematics. Kemp has suggested that this preference may have been two-fold, both in Leonardo’s own limited abilities at mathematics and algebra but also as an intellectual preference for a more fluid model of a dynamic world based on the beauty of proportions, interrelations and first-hand experience of the world. Leonardo referred to geometry as “the science of continuous quantity’” whereas he referred to numbers and mathematics as dealing with “discontinuous quantities” with little correspondence to the nature of actual physical forms. (6) In his essay for the book accompanying the 2006 exhibition 'Leonardo da Vinci: Experience, Experiment and Design' at the Victoria and Albert museum in London, Kemp discusses Leonardo’s use of disegno as a means to think visually. Disegno was a common term used by Renaissance draughtsmen and is normally translated in English as either drawing (in a fine art context) or design (in the context of applied arts). Leonardo’s use of disegno allowed him to integrate the subjective imaginative faculty or fantasia with the intellect, which in turn achieved expression in the Renaissance concept of science (scientia). Misura was the term used to describe the measuring of proportions, the construction of perspective systems and rules of light and shade, and was regarded by Leonardo as the fundamentally scientific aspect of expression in painting. (7) In works such as the Perspective study for the adoration of the Magi (figure 6), we can see this process at work in the way he combines the fluid, creative, subjective process of disegno with the logic, rigor and measurement of misura. Kemp uses the following quote from Leonardo to support his claim that disegno was considered as the supreme tool that served the eye as a means of investigation and exposition. When Leonardo praises how the eye commands the hand, Kemp suggests that he was essentially making claims about the power of disegno: "Now do you not see that the eye embraces the beauty of the world? The eye is commander of astronomy; it makes cosmography; it guides and rectifies all the human arts; it conducts man to various regions of the world; it is the prince of mathematics; it’s sciences are most certain; it has measured the height and size of the stars; it has disclosed the elements and their distributions; it’s made predictions of future events by means of the course of the stars; it has generated architecture, perspective and divine painting. Oh excellent above all other things created by God… And it triumphs over nature, in that the constituent parts of nature are finite, but the works that the eye commands of the hands are infinite." (8) 8) Codex Arundel, circa 1480 - 1518 (See below for a link to a digitised version) However, it's immediately notable that the systems Leonardo is praising, all relate to the power of diagrams, diagramming, and diagrammatic thought processes, and this becomes even clearer if we consider the examples he refers to: astronomy and celestial charts, the theory and practice of the systems of proportions governing artistic beauty, cosmography (9), cartography and navigation, mathematics including trigonometry and geometry, the analysis of dynamic and static systems in the behavior of earth, water, air and fire, architectural plans, elevations, sections and systems of perspective and the ‘divine’ science of painting with its ‘roots in nature’. Drawing and thinking through diagrams was for da Vinci a natural, almost instinctual means to develop his ideas, communicate them with others and construct a science of painting. However, as with other artists of the Renaissance, Leonardo inherited the tradition for diagramming from Medieval diagrammers before him, as I covered in previously blog posts: Diagrams from the Dark Ages, and Cosmic Diagrams from Alchemical Laboratory. Leonardo's online Codex:Leonardo's Codex Arundel consists of 570 images of dense cryptic notes surrounding technical diagrams. The 283 page manuscript was digitized in 2007 as a joint project between the British Library and Microsoft called “Turning the Pages 2.0,” and can be accessed by clicking here. The Alternative Vitruvian Men: |
|||||||||||||||||||||||||
|
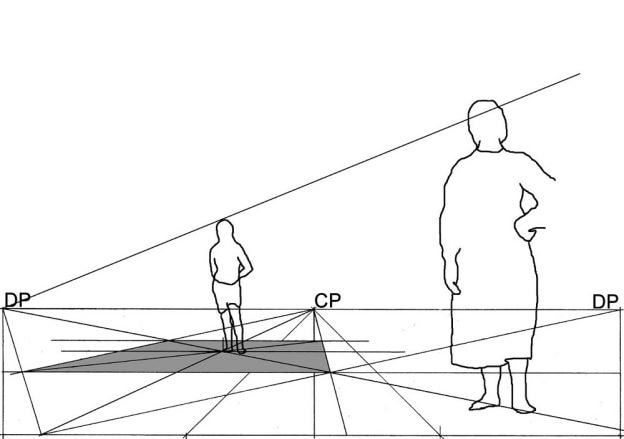
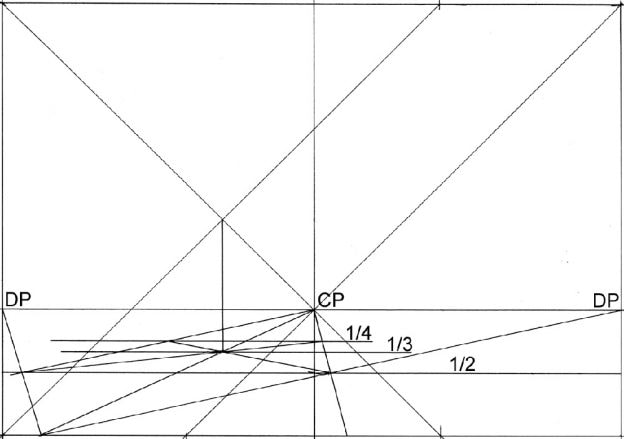
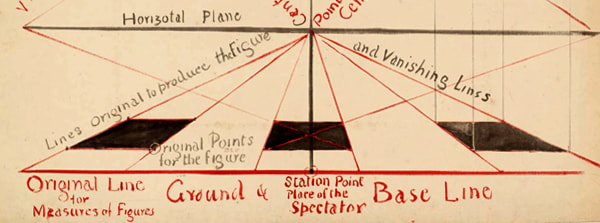
"Essentially, perspective is a form of abstraction. It simplifies the relationship between eye, brain and object. It is an ideal view, imagined as being seen by a one-eyed, motionless person who is clearly detached from what he sees. It makes a God of the spectator, who becomes the person on whom the whole world converges, the Unmoved Onlooker."
Robert Hughes (2)
|
RT: I did, but realized early on that I had chosen the wrong subject. I noticed also that
you had studied Biomedicine.
MW: Yes, so I was immersed in diagrams, especially as I specialised in Biochemistry, which as a subject deals with diagrams on many levels.
RT: Yes, when I was at school, all the chemistry diagrams and the glassware we used, I still find very exciting, it still gives me a buzz when I look at those diagrams. Also I suppose that Alchemical drawings which are in a sense diagrammatic, but which also refer to broader cultural aspects and spiritual things. But I think it is that combination of diagrammatic mixed with something else where things become very interesting.
MW: Especially for the initiated few who can decode and read the Alchemical imagery and illustrations such as those in Michael Maier’s books. And you were also interested in optics and optical diagrams ?
Figure 2: Ray diagram from 'OPTICKS:
A treatise of the Reflections, Refractions, Inflections and Colours of light', Sir Isaac Newton
(forth edition, 1730, Available online here)
MW: That’s something I wanted to ask you about because you had mentioned that you were interested in landscapes, and the idea that maybe the drawings you make are detached, conceptual landscapes. I remember reading 'To the Lighthouse' by Virginia Woolf, and there’s a very short chapter in the middle of the book, which describes time passing in an empty room. But it does so from outside the book, from the detached perspective of an omnipotent narrator, an all seeing eye. I wondered if that was something you were interested in as an artist?
RT: Yes, I think so. I suppose maybe it’s this kind of hyper-consciousness, just this thing, observing, and you just become very aware of time and space, and of yourself as a little entity within this. It’s almost as if time disappears.
The other thing I remember reading a lot as a student was Nietzsche, and the image of time as a snake eating its tail. He called it ‘eternal recurrence’, where you’re trying to imagine that every moment could be relived exactly the same, so it kind of neutralizes time, because as animals we’re stuck with this as a problem and try to find strategies to overcome that sense of things in the future and things in the past.
MW: I read that time was something that you would like to take out of your drawings, or perhaps avoid referencing in some way. Also, that you presented the objects in your drawings as Platonic forms, without any signs of wear and tear or reference to scale.
RT: Yes, that’s right, I started off by making objects, but always found it really frustrating in terms of size, or what you make it with. But I suppose that a lot of the twentieth century was about that problem, about objects, and their separateness to us all.
MW: Such as the use of Plinths to present work ?
RT: Yes, for example Plinths.
MW: So did you ever regard your sculptural works as models, as a way to perhaps overcome these issues ?
RT: I suppose I did think of them as 3 dimensional diagrams, but then I suppose that made me unhappy about the materials they were made from. I always imagined whether perhaps it could be made out of perfect marble perhaps.
MW: I started to consider making works from elemental materials, such as aluminium or carbon, just to try to deal with the problem of simplifying or neutralizing that issue of materiality. One of the 3 dimensional works that you made called ‘boat’ was made out of rubber wasn’t it ? Hanging as a collapsed frame on the wall, the skeletal form of a boat.
RT: Yes, it’s funny that that particular series of works didn’t end up going anywhere; I’m just trying to remember what the actual sequence was.
I think sometime in the early eighties, I was put forward for a commission; it was one of those completely random invitations to do something. It was for the Savoy Hotel. It was one of those awkward things of, well, do you design sculpture, or do you use something you’ve already got? So I started playing around with drawings and making cutouts from drawings of things. I ended up with some large sheets of rubber and started cutting it out to see whether it was something I could use.
I didn’t intend to end up with something which would hang on the wall, but I did that in the studio by putting it to one side, and it’s quite extraordinary how that works. So it was quite accidental, but was just the recognition of having taken it in to that different area that I didn’t have any control of, so it was quite accidental. It was all cut by hand, so it was a very crisp line cut with a scalpel.
MW: About your working process, you wrote very beautifully about that initial process of orientation, the initial white sheet that you approach, and the infinite possibilities you’re faced with - setting up some kind of initial starting conditions. You used the analogy of the Gothic Cathedral with its ground plans, and then the more organic process of construction that follows that.
There was also another article in the same book (Writing on Drawing: Essays on Drawing Practice and Research) by Terry Rosenberg about ideational drawing, a process of drawing which I though really suited your work very well.
RT: Yes, I mean I must say that I haven’t read fully all of the articles in that book, but have skimmed through them.
MW: There were a couple of essays that really stood out for me personally, yours and Terry Rosenberg’s. I enjoyed the way you talked about your use of perspective, not as a tool to create realistic drawings, but as a tool to allow you to use your intuition.
RT: Well I think that also goes back to that idea of self-consciousness, sort of knowing that you’re this entity that looks at something from the outside.
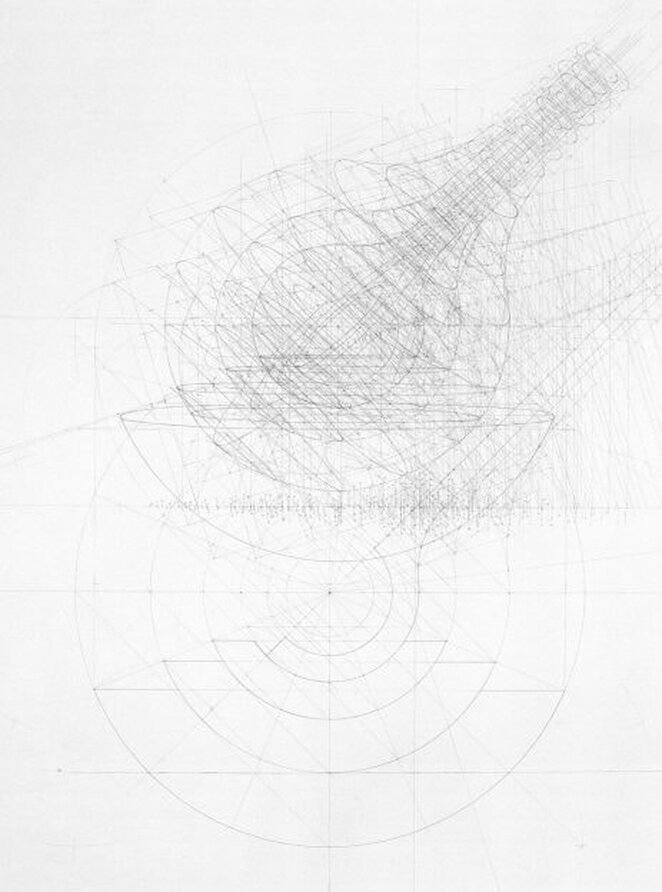
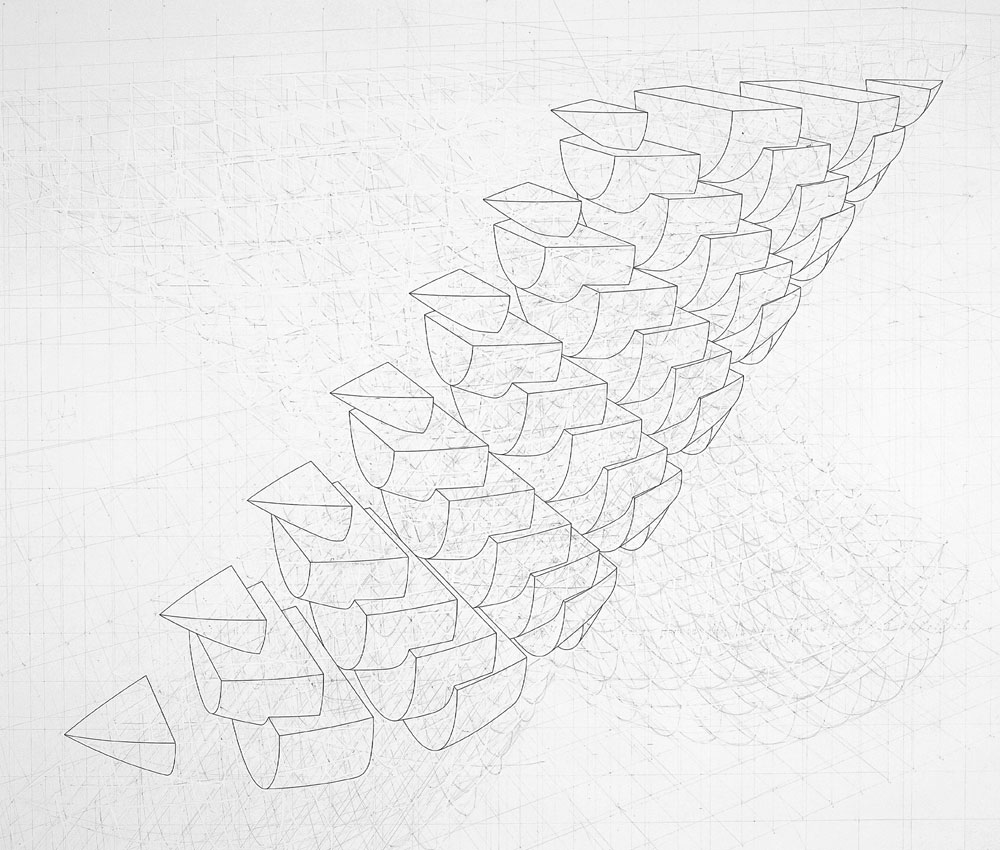
I used to play around with spatial perspectives, and then I thought that actually one way of neutralizing these issues was just to use it, just to actually use the system. So that to get over that whole issue of viewpoint, for example when you make a piece of sculpture, how do you look at it ? If there’s no best side as it were. So I thought, well if I just take it on full, this issue of perspective, and to absolutely use it as it was set up to use, then it falls by the way side, as an issue.
MW: Turning the problem in to part of the solution?
RT: I think it’s like sometimes in Mathematics, when a problem can’t be solved directly, they will call on a tool from other part of mathematics, and using that tool they can then move from one place to another. But in the end result, that tool disappears, it doesn’t ultimately play a part in the answer, but it has been a useful tool to get you from one place to another.
MW: That reminds me of the role enzymes play in Biochemistry. They’re completely essential to facilitating the process, but don’t take part in a reaction in a way that they are altered themselves in the outcome.
RT: Yes, that’s right, yes. So it is a kind of a vehicle, but then it’s using that perspective that makes me then question how it was originally used in the Renaissance, because when you’re actually working with it on the paper, there are so many interesting things actually going on that art historian looking in from the outside wouldn’t grasp. And it is to do with that idea of play, between the diagrammatic and the spatial element. Perspective isn’t all about creating a space, it is about the surface and how these things operate 2 dimensionally as well.
MW: I was very interested in the way you talked about the depth of space in your drawings, and not using deep space, but keeping things relatively shallow and immediate.
RT: Yes, I think that this also relates to my sense of what these Renaissance artists were doing. The picture that is portrayed of perspective is all about getting everything in terms of the horizon. But I don’t actually think that’s it at all. You are really working in a really shallow space. All those Renaissance paintings are also working in a really shallow space, and I think when you’re actually constructing that on the paper, there’s a real, almost physical connection to the space.
MW: I don’t normally use colour in my work, it’s actually something I avoid, and have for a long time. Then I came across a book by David Batchelor called Chromophobia. He was writing about colour and how it has been perceived as the additional, the exotic, the lipstick. Or at least that’s how it was regarded by artists and writers who saw it as extraneous. And so I’m interested to ask you how you deal with colour in your work.
RT: Well I have to admit as to having always avoided it, as I’ve never understood it. It’s a complete mystery. If I was making a drawing, I can’t see any reason to use colour. But then equally I probably can’t see any reason not to use it. But then I would probably be thinking well, why do I ? But then I know with somebody like Michael Craig Martin, I suppose he’s somebody in the seventies who was producing very austere, paired down work, such as his linear drawings, which were initially all black and white.
But then he probably just stopped worrying and started to use incredibly strong colours in his work. And now the colour is really significant to his work. But its interesting that Michael Craig Martin was taught by Joseph Albers.
MW: That’s interesting, I didn’t know that.
RT: Yes, at Yale. So he would have had a real grounding in colour, and it’s almost as if he, you know – 30 years later or whatever it was – just decided to start using these colours. It is odd how we set rules for ourselves and at the time we kind of need them, but occasionally we just think ‘drop them’, and stop worrying about them.
MW: There were a number of times when looking at your works and reading what you wrote about them that reminded me of mathematics, and the idea of skeletonized forms. The idea of an equation, where the aim is to remove as much information as possible and leave only the knowledge - the process of essentializing something. Also the way that you talk about using intuition, and how intuition can be very immediate, or how it can require you to put the work away for many years. A slow boiler that you come back to much later.
Is mathematics something you’re interested in? Or is it restricted to geometry, or patterns of thought?
RT: Yes, I’m interested, not in the sense of reading books on mathematics, but when I’m near mathematicians and they talk about what they are doing, I do feel an affinity with what they are doing, and I suppose that with my drawings, they become very complex, but I do have that hankering after something really, really simple. I do have this idea that one day I’ll just be able to draw a line, and that that will be the finish! And in a way I suppose you do occasionally see it in some art works – and think that that is just an extraordinary piece of drawing, but then that in a way embodies everything they’ve ever done – 40 years later they’ve managed to make this extraordinary thing !
MW: Richard Dawkins wrote a while ago about the idea of a conceptual space containing all possible genetic variations, a kind of hyper-space of all possible genetic forms, and I was always fascinated by that idea. I think that also Douglas Hofsteader in Goedel Escher Bach, described the idea that Bach, in composing, had the ability to look over all the millions, well almost infinite combinations of musical notes, and was able to see patterns, islands or constellations of musical forms. And I wondered if that idea was perhaps something you were interested in. A vaguely discernible, fuzzy possibility of the form you’re searching for, and how this idea relates to diagrammatic forms.
RT: Yes, I think that is definitely true, and I suppose that one of the things I am aware of is that in some ways, the drawings all start from the same point. That blank paper, that orientation.
MW: The tabula-rasa ?
RT: Absolutely, and you know that it could go in a completely infinite number of directions, and yet there is a sense that there is some solution there - that you setting things up. It becomes very obvious sometimes.
I wouldn’t compare myself to Bach, but I can see that way of thinking - that there is an infinite number of possibilities, but you alight on a particular form that is true for you in one sense or another. It’s hard to really articulate that process.
RT: I think when I first started using perspective I was still in that mindset of drawing objects as things in space, but then quite quickly I became aware of how potent the workings-out - you know, the plans, the elevations and so on - how potent they were and how they were working with the kind of forms which were being described. It was also in trying to pin things down, I became aware of the balance between leaving things open ended and tying something down and saying ‘this is that form’. It was that form, but not in such a positive or fixed way.
I stopped using ink on the drawings. I was using ink to go around the forms I was building, but that stopped. And so I started getting a much more subtle interplay between the workings out, and those workings out would be the plans, and elevations, and a myriad of other kind of connections which were being built, a kind of scaffolding.
MW: And you saw inking in as a kind of finishing process ?
RT: I did. You know you suddenly think that it has in a way killed off the drawings. Not inking became a way to leave the drawing as an open-ended thing. Perhaps when a work is too ‘closed down’ it can end up being very uninteresting. For example Raphael. I’ve never enjoyed looking at Raphael’s paintings because they seem so overly fixed, whereas, Piero de la Francesca’s paintings seem almost as if they are propositions.
Oil and tempera on panel, 58.4 x 81.5 cm
The Flagellation of Christ (outline and outline proportions)
Courtesy of Richard Talbot.
MW: Very early on in coming up with the questions that I wanted to ask in my PhD, I pretty much hit the same problem you did in realizing that I had always studied sculpture, but always made drawings. And I thought of the drawings as sculptural drawings and, luckily for me, my teachers at the time thought the same. So I had to decide whether to investigate the relationship between 2D and 3D diagrams - and thus include sculpture, or the way in which artists use diagrammatic image making to a romantic end, a subjective end; the way in which Marcel Duchamp played subject against object and also struggled with the issues of dimensionality. Where do you stand in terms of subject and object ?
RT: Yes, well I don’t think I would come down either way, because I don’t think that coming down on either side actually gets you anywhere. I suppose that in my student days, this dilemma about the objective and subjective was helped by there being, at Goldsmiths - which was something which was great about Goldsmiths at that time - was that there was a huge range of practice within the staff.
So you did have conversations with people who were systems thinkers, right through to people who were watercolour, or landscape painters. People weren’t trying to ram the stuff down your throat; you were just having these interesting conversations, and then weighing it up about your own situation.
Thinking about what you were doing, what you thought you were trying to do, what you were actually doing ! You know, all those worries you have about, you know, ‘is it art ?’ I found myself really being able to make work when I stopped worrying about what side of the fence I was on, and finding a way of working where I felt as if I wasn’t having to choose one way or the other. But both sides of me could be involved in that hankering after perfection. It’s a case of playing these things off against each other.
I distinctly remember that when I did my MA at Chelsea, the external assessor we had was Paul Neagu, I think he’s dead now, but he was very well known. He was one of the artists who Richard Demarco brought to this country, alongside such artists as Joseph Beuys.
Anyway I remember that the work I’d made at Chelsea had become really quite austere, and extremely minimal, and he said… ‘don’t forget the other side of yourself’, and I realized exactly what it was he meant. That we can easily kind of forget. But then I think that also we need those extremes sometimes, to realize something. We need to go beyond in order to know where the edge was. It’s only when you fall over the edge that your realize there was one !
MW: So there is actually nothing within your body of work that you see as a mathematical proof, some foundation to build upon ?
RT: No, I would certainly never say that there is anything that I’m demonstrating that is mathematical, no. I could say that when I was at Goldsmiths, I was taught by people who were involved in systems, and there were several people I knew, for example Malcolm Hughes working at the Slade, who had students working with experimental systems, building computers to generate paintings and so on; and I always felt that there was a problem in that they knew the kind of thing they were aiming for, and that it just seemed as if, well, you could make that painting without that system.
It was almost as if they were using that system as almost a ‘get out’. The paintings would always end up looking like lots of other abstract constructive paintings that weren’t made with a system, that were just made purely intuitively. And so I have a distrust of the idea of a system, and I think that that system is always, ultimately being driven by you.
MW: What are you working on at the moment ?
RT: Well apart form being heavily tied up in administration, I’ve finished some drawings and I’ve also been playing with film and video, which I can show you if you want.
It’s very long drawing, based on a system in a sense, and was a definite play on the standard idea of a single viewer’s perspective. They start with a really basic perspective grid, a ‘unit’, drawn in such a way that I can simply add these units together and extend the space in any direction. Strangely, it adds the possibility of time, in that your eye can travel along the drawing and the space continues always to make sense.
The video is another simple grid that is constantly shifting from the 2 dimensional surface in to the 3 dimensional image. Originally I had intended it to be projected on to a screen, but then I had the chance to project it in one of the large spaces downstairs, and the results were quite extraordinary - because it did actually become part of the space, which wasn’t fully intentional, but those were the results.
The question of the artist’s intention is also an interesting problem I think within the history of perspective; the well-known analyses of key renaissance paintings demonstrate that the spaces in the paintings are sometimes not quite what they seem to be. There is often some uncertainty, yet it is usually thought that perspective is fixed - that it's an unambiguous and rational thing.
MW: Watching the video feels like a trying to solve a puzzle in perspective, there are moments when the lines are like a 2 dimensional pattern of shifting compositions, and then suddenly something in the visual cortex takes over and there’s the impression of instant depth from those very same lines. It reminds me of watching animations of higher dimensional cubes rotating. You think you have understood what is happening and there’s a sudden unexpected shift, you have to grapple with different kinds of depths.
RT: Well - I don’t know - It’s to do with my intention, I’m not settling down to produce something which has a specific result. I know they do result in that, but I’m not setting out to do that.
I am showing this work – I’ve never tried it before. I hope it works… It’s actually going to be projected on to three screens, the same image, butted up against itself, but slightly out of synch. So the whole thing will be ‘shifting’, so that a more complex thing will be going on. I have no idea what it will look like – it might just look awful, but then I’m trying it – for this show.
Grid from Richard Talbot on Vimeo.
Richard's academic studies in to the origins of linear perspective can be downloaded by clicking on the following link:
| speculations_on_the_origins_of_linear_pe.pdf | |
| File Size: | 3315 kb |
| File Type: | |
Finally, below are a series of Piero della Francesca's own diagrammatic studies from his book 'De prospectiva pingendi: a treatise on perspective' c 1470 - 1492. The treatise, divided into three books, provides detailed, mathematical instructions, illustrated with numerous diagrams, for creating realistic perspective in illustrations. It was widely known among artists (such as Albrecht Dürer), but also in an academic milieu, where the copies of the Latin translation are thought to have circulated.
The book is available to view online at the British Library here.
1) Talbot,R. (2008) Drawings Connections, In: Writing on Drawing: Essays on drawing practice and research (2008) Intellect Books, UK: Bristol, p.55.
2) Hughes, R. 1980, The Shock of the New, London: Penguin Random House Company, p.17.
for Paul Eluard's book of poetry 'Repetitions', published 1922
without the help of a good drawing,
is not only half a mathematician,
but also a man without eyes. "
Lodovico Cigoli to Galileo Galilei, 1611
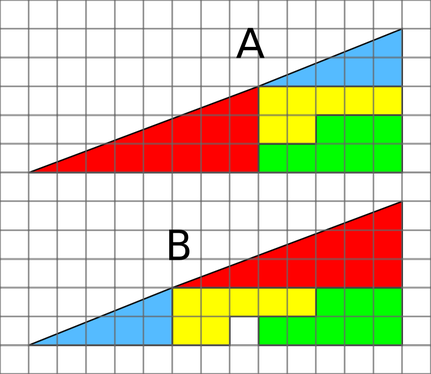
A number of simple, cautionary examples of the problematic relationship between Maths and diagrams exist as diagrammatic puzzles, and a famous example is the 'Missing Square Puzzle' shown in figure 1.
| Figure 1: When component parts of triangle A are rearranged, an empty square appears from nowhere | When the coloured components of Triangle A are rearranged to form Triangle B, the process of their reorganisation creates an empty square from nowhere, despite the fact that both triangles appear to have identical surface areas. The key to understanding this kind of puzzle is the idea that Mathematical objects exist in a fictional world created by mathematicians. No matter how precisely drawn, Geometry diagrams only ever give rough approximations of the ideal objects they represent, and these objects can only ever exist in a world where points has zero dimensions and where a lines and planes have zero thickness. |
Marcel Duchamp was fascinated by the idea of a parallel world of Mathematical perfection that exists alongside the chaos and imperfection of reality and daily experience. This was the subject of the blog post: 'A soggy book of diagrams as a wedding present from Marcel Duchamp', which considered one of Duchamp's less well known projects using a found book of Euclid's Geometry.
| Figure 3: Mitsunobu Matsuyama's 'Paradox' | Another excellent example of this type of diagrammatic puzzle is the Mitsunobu Matsuyama Paradox, which consists of a square divided into 4 quadrilaterals. When each quadrilateral is rotated 90 degrees clockwise, the new arrangement suddenly gives rise to a small central square, as depicted in red in figure 3. This puzzle also relies on the natural limits of accuracy to human vision. Both the height and width of the two squares (before and after rotation of their quadrilaterals) are fractionally different, but this is barely distinguishable to the naked eye, because the difference is spread around the entire perimeter of each square. |
For Lodovico Cigoli, a good 17th century diagram provided a visual means of gaining a deeper insight into the mathematics of nature. However, over the course of the following two centuries, the role of the diagram shifted to the extent that it became considered more of a veil that obscured the essence of mathematics, and algebra was proposed as the only way to lift the veil.
"...it is not the figures which furnish the proof with geometers, though the style of the exposition may make you think so. The force of the demonstration is independent of the figure drawn, which is drawn only to facilitate the knowledge of our meaning, and to fix the attention; it is the universal propositions, i.e., the definitions, axioms, and theorems already demonstrated, which make the reasoning, and which would sustain it though the figure were not there." (2)
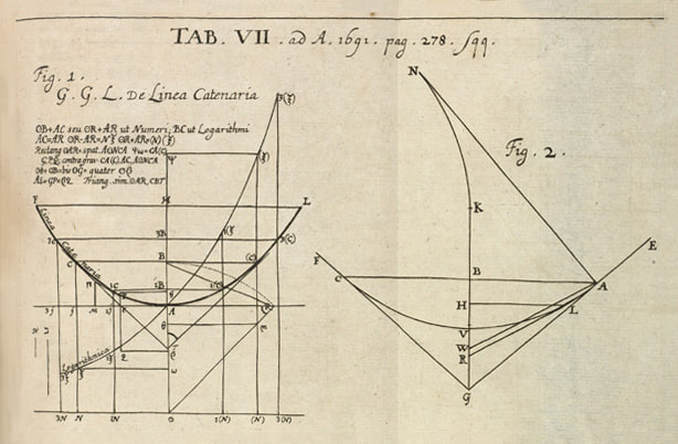
by Gottfried Leibniz (Figure 1 left) and Christiaan Huygens (figure 2 right) to Jacob Bernoulli
for publication in the Acta Eruditorum, 1691
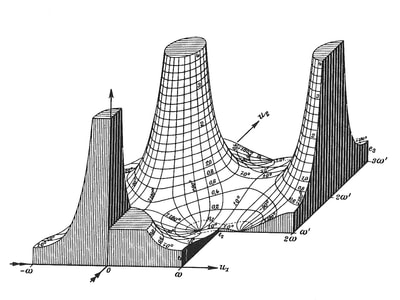
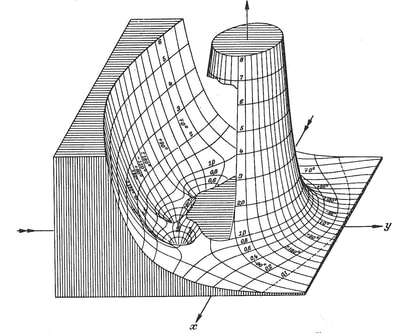
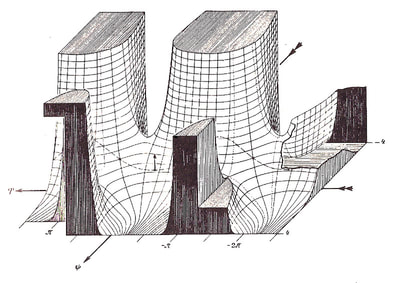
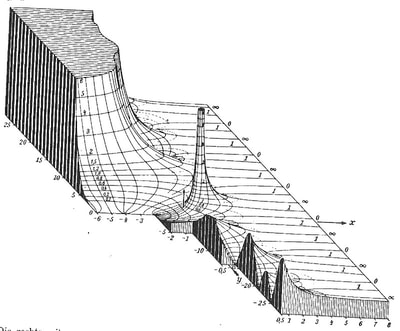
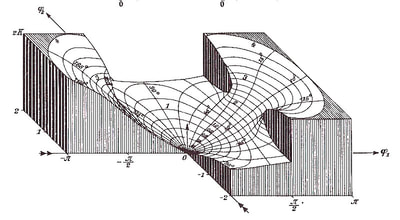
However, the diagram remains an extremely powerful tool and a visual guide in providing an insight into the austere and pristine world mathematical geometry and topology. Leibniz's own notebooks contain an astounding array of diagrammatic sketches that accompany his mathematics, as in figure 4, and the designs and calculations for his 'Universal Calculator', some 200 years before the work of Charles Babbage.
For an interesting introduction to the notebooks of Leibniz, see Stephen Wolfram's blog: Dropping In on Gottfried Leibniz.
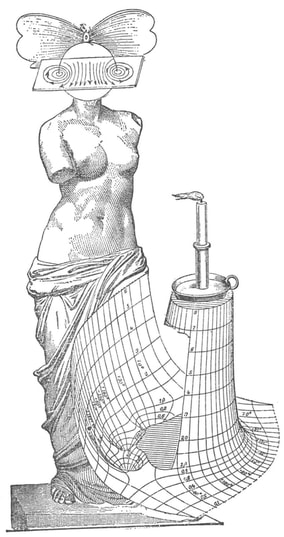
Man Ray described the models that he found languishing in dusty cabinets as 'so unusual, as revolutionary as anything that is being done today in painting or in sculpture', though he admitted that he understood nothing of their mathematical nature. When the Second World War came to Paris in 1940, Man Ray relocated to Hollywood, where he started work on a series of 'suggestively erotic paintings' based on his 1930's photographs. Under the title of the 'Shakespearean Equations', he later referred to the paintings as one of the pinnacles of his creative vision.
Below are images of selected paintings from the 'Shakespearean Equations' series, Juxtaposed alongside the original mathematical models they were based upon.
Note: An extensive online collection of mathematical models is available here: the Schilling Catalogue of Mathematical models
shown alongside the models they were based on, from the Institut Henri Poincaré, Paris.
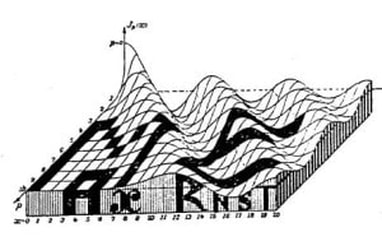
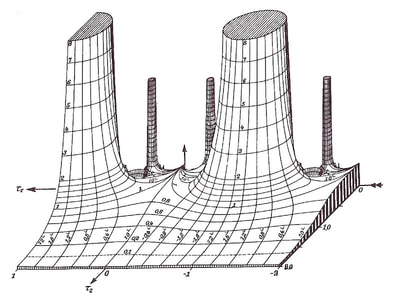
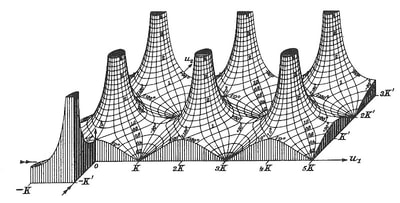
As Witt points out in his own blog on this series here: Functional Surfaces I, it's said that the architect Le Corbusier kept a copy in his studio whilst designing the Phillips Pavilion. Max Ernst appropriated from the book for a series of collages and poems in the catalogue accompanying his 1949 exhibition 'Paramyths'.
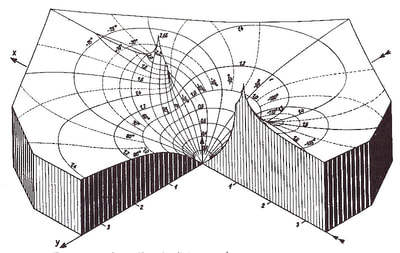
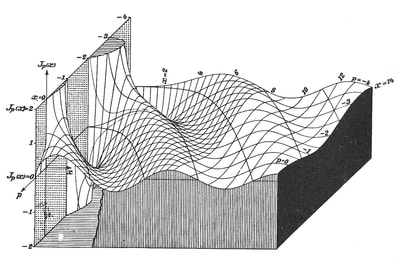
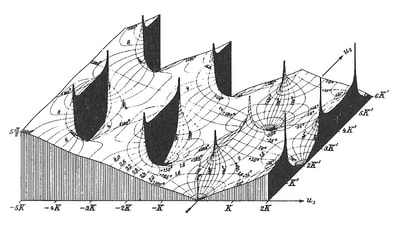
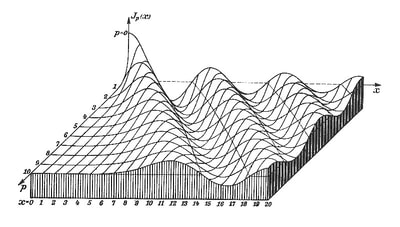
| Figure 6: La Fable de la Souris de Milo (The Fable of the Mouse of Milo), Max Ernst, Collage, c.1948 | The graphs used by Ernst in figures 6 and 7 represent Bessel functions, prescribed solutions to differential equations found to govern a variety of wave motions, particularly those that are confined to the surface of spheres and cylinders. The head of the venus de Milo in figure 6 also contains diagrams of electromagnetic and planetary gravitational fields. Figure 7: Ausstellungssignet, Max Ernst, 1948 Pen and Ink on Paper, 5.6x10.5 cm. |
by Eugene Jahnke and Fritz Emde, courtesy of Andrew Witt.
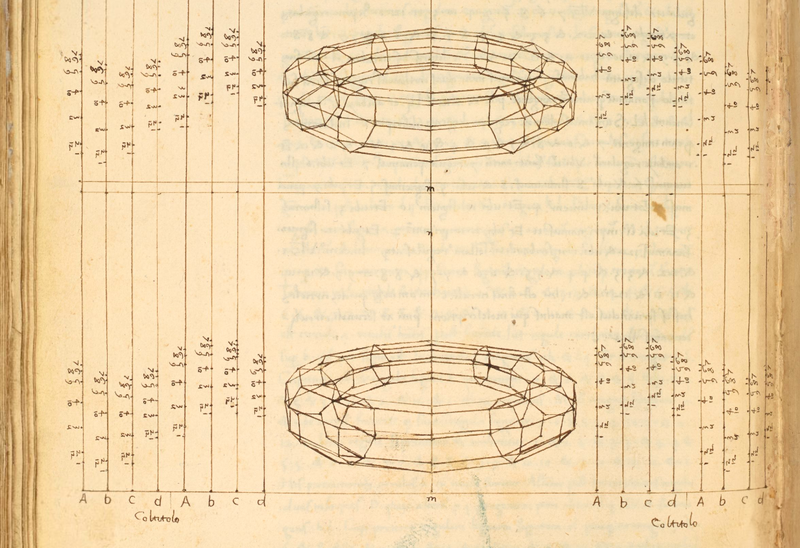
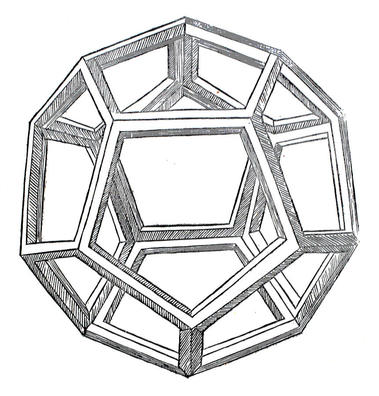
| Dodecahedron planum vacuum, Lithograph by Leonardo da Vinci, for Luca Pacioli's 'Divina Proportione', 1509. | The dynamism and immediacy of computer rendered models has abruptly changed the way we experience the geometrical diagrams of Mathematics. The video below was made by the Mechanical Engineer and amateur Mathematician Jos Leys using POV-Ray. The film opens with a rotating 600 cell (a 4 dimensional analogue of an Icosahedron), before dissecting and reconstructing a 120-cell (a 4-dimensional analogue of a dodecahedron) in twelve rings of 10 dodecahedra. Two sets of six rings form 2 solid interlocked tori. More video and information available here: JOSLEYS.COM |
a dissection of the 120-cell in 12 rings of 10 dodecahedrons
1) Some 29 letters from Cigoli to Galileo remain, however only 2 letters from the scientist to the painter are left, as the artist's heirs chose to destroy all incriminating evidence of their association, after the papal condemnation of Galileo. (In 1610 Cigoli received from Pope Paul V the assignment to paint the dome of Santa Maggiore Maggiore with the Immaculate Conception, the Apostles and Saints.)
2) Leibniz1704, New Essays: 403
The diagrams of geometry - part 2: A soggy book of diagrams as a wedding present from Marcel Duchamp
10/20/2016
Feel free to leave comments or to contact me directly if you'd like any more information on life as an artist in Japan, what a PhD in Fine Art involves, applying for the Japanese government Monbusho scholarship program (MEXT), or to talk about diagrams and diagrammatic art in general.
in front of Network of Stoppages (1914),
Oil and pencil on canvas, 148.9 x 198.12 cm
We have already seen in a previous post how Duchamp's training as a young artist was founded upon the diagram, having studied during a period in France when students were made to practice mechanical drawing as opposed to the traditional historical modes of figurative and landscape.
Trained in ‘the language of industry’, (2) Duchamp remained fascinated with the detached, objective qualities of technical diagrammatic drawings, proclaiming his desire to create “paintings of precision” with a “beauty of indifference.” (3)
He also spoke in interview of how he wished to "go back to a completely dry drawing, a dry conception of art. I was beginning to appreciate the value of exactness, of precision and the importance of chance… And the mechanical drawing was for me the best form of that dry conception of art… a mechanical drawing has no taste in it. (4)
|
Figure 2: Marcel Duchamp, Chocolate Grinder (No. 1), 1913, Oil on canvas, 61.9 x 64.5 cm
© Artists Rights Society (ARS), New York / ADAGP, Paris / Estate of Marcel Duchamp |
Figure 3: Marcel Duchamp, Chocolate Grinder (No. 2), 1914, Oil, graphite, and thread on canvas,
65.4 x 54.3 cm © Artists Rights Society (ARS), New York / ADAGP, Paris / Estate of Marcel Duchamp |
The steps Duchamp took to refine his work towards being beautifully indifferent images of precision are visible in the two paintings above, made within a year of each other. Chocolate grinder number 1 (1913) is painted in traditional perspective and the illusion of three dimensionality also relies upon its strong shadows and graded colouration. On the other hand in Chocolate grinder number 2, the object is depicted in what could be described as a conceptual landscape: a neutral and shadow free environment of flat colour and a strict one point perspective.
Despite his fascination with the diagram Duchamp continued to seek out new ways to subvert this mechanical, ‘anti-expressive’ system of geometrical depiction on a number of levels, such as his attempts to incorporate chance and chaos in to his artistic process.
In "Three standard stoppages", the artist claims to have dropped metre long pieces of string from a height of one metre and traced the outline they made upon landing. These shapes were then cut out of strips of wood and presented in a box as a set of alternative, two dimensional standard metre lengths.
1913–4, replica 1964, Wood, glass and paint on canas, 400 x 1300 x 900 mm
It is important to take into account what was happening within the world of science at the time these works were being made, and Duchamp's active interest in the popular science books of the time.
In "Science and Hypothesis" (1902) for example, the mathematician, theoretical physicist, engineer, and philosopher of science Henri Poincaré posed the question of whether or not it would be 'unreasonable to inquire whether the metric system is true or false?'. At almost the same time, two other noteworthy figures Hermann Minkowskiand Albert Einstein were already setting about redefining our most basic understanding of the very geometric fabric of reality for the first time in well over 2000 years. (6)
Also of special interest to Duchamp at that time was the work of the French humorist Alfred Jarry (1873-1907), creator of Pataphysics, or the 'science of imaginary solutions'. Jarry developed this imaginary subject to "examine the laws governing exceptions, and … explain the universe parallel to this one", and it is easy to see how Duchamp was drawn to such a novel, humorous and profoundly revealing idea with its suggestions of alternative realities with their own physical laws. (7)
The wooden templates of Duchamp's "diminished metres" were later used to design the pattern of lines in his painting "Network of Stoppages" (Reseaux des stoppages), shown below.
1914, oil and pencil on canvas, 198 x 149 cm
|
Figure 6: Marcel Duchamp, Young Man and Girl in Spring, oil on canvas, 1911
|
A similar "Romantic - Objective" contrast was made when the artist later transferred his diagrammatic network to his master work "The Bride Stripped Bare by her Bachelors, Even (The Large Glass)" 1915–23, another major work of Duchamp's that is fundamentally diagrammatic in nature. |
The large glass subverts the dry, mechanical visual language of objectivity by applying it to subjects that it wasn't designed to address, namely the psycho-sociology of human courtship and sexuality, or what would previously have been called romanticism.
[Due to the complexity and art-historical importance of The Large Glass and its accompanying notes, it will be covered in a future post dedicated to that work alone.]
Foreshadowing the production processes of Sol LeWitt, Unhappy Readymade consisted of a simple set of instructions sent by post as a wedding gift to his sister Suzanne Duchamp and the artist Jean Crotti, so that, in the words of LeWitt, “the Idea becomes a machine that makes the art.” (8)
In an interview with Pierre Cabanne, Duchamp described his instructions for Crotti to buy a
"…geometry book which he had to hang by strings on the balcony of his apartment in the rue Condamine; the wind had to go through the book, choose its own problems, turn and tear out the pages. Suzanne did a small painting of it, ‘Marcel’s Unhappy Readymade.’ That’s all that’s left, since the wind tore it up. It amused me to bring the idea of happy and unhappy into readymades, and then the rain, the wind, the pages flying, it was an amusing idea… " (9)
|
Fig. 7: Unknown artist, Photograph
of Unhappy Readymade, 1920 |
Fig. 8: Suzanne Duchamp, Unhappy Readymade, oil on canvas, 1920
|
Fig. 9: Marcel Duchamp, Unhappy Readymade, Box in a valise version, re-touched photograph, 1935 - 41
|
The Duchamp scholar Linda Dalrymple Henderson points out that this was in fact one of the artist's last specific comments on geometry, and that the book used was a copy of Euclid’s elements so that, ironically, the plane geometry of Euclid was in contrast to damage caused by the wind and rain producing distortions in the diagrams as “non-Euclidean deformations of the Euclidean geometries in the text.” (10)
In a letter to his sister, Duchamp wrote: “I liked the photo very much of the Ready Made sitting there on the balcony. When it all falls apart you can replace it.” (11)
Duchamp also suggests that this is a lesson to be repeated, a reminder of the fundamental difference between an essentialised, idealised, conceptual landscape of perfect forms, and the chaotic nature of decay and change, which composes our everyday experience of the real world. Some years later Duchamp told one interviewer that “he had liked disparaging ‘the seriousness of a book full of principles,’ and suggested to another that, in its exposure to the weather, ‘the treatise seriously got the facts of life’”. (12)
Downloadable copies are available in various formats courtesy of an Internet Archive at the University of Toronto Libraries here: Downloadable formats
Or as a pdf here: Downloadable pdf.
Click on the pages of the book below to turn them:
Oliver Byrne (1810–1890) was a civil engineer and prolific author of works on subjects including mathematics, geometry, and engineering. His most well known book was this version of ‘Euclid’s Elements’, published by Pickering in 1847, which used coloured graphic explanations of each geometric principle.
The book has become the subject of renewed interest in recent years for its innovative graphic conception and its style which prefigures the modernist experiments of the Bauhaus and De Stijl movements. Information design writer Edward Tufte refers to the book in his work on graphic design and McLean in his Victorian book design of 1963. In 2010 Taschen republished the work in a wonderful facsimile edition. ( Wikipedia link )
1) Nayral, J. (1912) preface to Galeries J. Dalmau, Barcelona. Exposció de Arta cubista. (April – May 1912) Reprinted in Guillaume Apollinaire: Les Painters Cubistes. Breunig, L.C., Chevaliare J. Cl. Paris: Hermann (1965) p. 181
2) Nesbit, M. (1991) The Language of Industry. In: The Definitely Unfinished Marcel Duchamp. De Duve, T. (Ed.) Massachusetts: Cambridge: The MIT Press, 1991. pg.356.
3) Duchamp, M. Salt Seller: The writings of Marcel Duchamp (Marchand du sel). Eds. Sanouillet, M. Peterson, E. New York: Oxford University Press, 1973. p. 30.
4) Duchamp, M. As quoted in Sweeney, A conversation with Marcel Duchamp, NBC Television interview, January 1956. Sweeney, J.J. (1946) Eleven Europeans in America: Marcel Duchamp. Museum of Modern Art Bulletin 13, p. 19-21. In: Dalrymple Henderson, L. (1998) Duchamp in context: Science and technology in the large glass and related works. New Jersey: Princeton University Press.
5) Duchamp, quoted in: Katherine Kuh, The Artist's Voice: Talks with Seventeen Artists, New York 1962, p.81.
6) Henri Poincaré quoted in: Herbert Molderings, 'Objects of Modern Scepticism', in Thierry de Duve (ed.), The Definitively Unfinished Marcel Duchamp, Cambridge, Massachusetts 1991, pp.243-65, reproduced p.247 Arturo Schwarz, The Complete Works of Marcel Duchamp, revised and expanded edition, New York 1997, pp.594-6, reproduced pp.594, 595, 596
7) Alfred Jarry quoted in: Dawn Ades, Neil Cox and David Hopkins, Marcel Duchamp, London 1999, pp.78-9, reproduced p.78
8) LeWitt, S. (1967) Paragraphs on Conceptual Art. Art Forum. June, 1967
9) Cabanne, P. (1971) Dialogues with Marcel Duchamp. Originally published: London: Thames and Hudson. p. 61.
10) Dalrymple Henderson, L. (2013) The Fourth Dimension and non-Euclidean geometry in Modern Art. 2nd Revised Edition. Massachusetts Institute of Technology. p. 283.
11) Duchamp, M. (1920) Letter to Suzanne Duchamp. In: Affectueusement, Marcel: Ten Letters from Marcel Duchamp to Suzanne Duchamp and Jean Crotti. (1982) Francis Naumann, M. Archives of American Art Journal, Vol. 22, No. 4. pp. 2-19.
12) Tompkins, C. (1998) Duchamp: A Biography. New York: Henry Holt and Co. Inc. p.212-214
Feel free to leave comments or to contact me directly if you'd like any more information on life as an artist in Japan, what a PhD in Fine Art involves, applying for the Japanese Government Monbusho Scholarship program (MEXT), or to talk about diagrams and diagrammatic art in general.
When the diagrammatic instructions are purchased, an accompanying certificate validates the authenticity of the artwork and grants the owner permission to reconstruct the work in a location of their choice.
By attributing absolute priority to concept LeWitt gave a Platonic dimension to these artworks, in that he insisted that they exist in essence as ideas in a purely abstract, immaterial way. In the words of LeWitt himself, “the Idea becomes a machine that makes the art.” (1)
Radically, LeWitt proposed that in order for an artist to deepen their artistic practice, they should aim to remove their individual subjective decisions and taste from the creative act itself. Again, in the words of LeWitt:
"If the artist wishes to explore his idea thoroughly, then arbitrary or chance decisions would be kept to a minimum, while caprice, taste and other whimsies would be eliminated from the making of the art… To work with a plan that is preset is one way of avoiding subjectivity… This eliminates the arbitrary, the capricious, and the subjective as much as possible." (2)
First Installation: LeWitt residence, New York (Art © 2011 The LeWitt Estate /Artists Rights Society, New York)
Lewitt's stance epitomises what I would now call that of the "Romantic Objective", in that his artistic practice successfully combines the idealistic goals of objectivity with poetic irrationality. (A much more detailed explanation can be found in Chapter 4.1 and 4.2 of my PhD thesis "Romantic Objectivism: Diagrammatic thought in Contemporary Art", which is available for download from the research page of this website.)
Looking at the first five propositions from LeWitt’s Sentences on Conceptual Art helps clarify his position, and how he conceives the role that intuition and logic play as devices with in his work:
1. Conceptual artists are mystics rather than rationalists. They leap to conclusions that logic cannot reach.
2. Rational judgements repeat rational judgements.
3. Irrational judgements lead to new experiences.
4. Formal art is essentially rational.
5. Irrational thoughts should be followed absolutely and logically. (3)
The diagrammatic format is central to LeWitt's practice and he used diagrams both to store his artistic concepts and then later translate and transcribe them into reality.
Imperfections that arise naturally during the process of recreating the works by hand, add a range of tones and textures to the images and, over time, Lewitt found ways to incorporate even this into the nature of the work, as shown in the time lapse video below.
The video was made during the installation of his wall drawing #797 at the Blanton museum of Art, in which minor imperfections become amplified due to repetition, adding to the unique character of the final work.
Black, red, yellow, and blue marker on wall Installation view, Feb. 2014
Blanton Museum of Art LeWitt Collection, Chester, Connecticut
© 2014 Estate of Sol LeWitt/Artist Rights Society (ARS)
" ...entropy of communication is reduced to the ideal state… in which the visual element is the exact result of a conceptual process [and] permits the extreme purification of the idea or concept, to the point at which it is presented for what it is, a rational and objective entity that does not admit those subjective or empathetic conditions that are part of the usual aesthetic operation. " (4)
Celant’s comments are idealistic in terms of the extent to which it is possible to strip an artwork entirely of its subjective nature, and are more suited to the early 'monosemic' works of the French conceptual artist Bener Venet, as we will see in a future post.
LeWitt's idealistic goal of objective image making lead him inevitably to the specialised visual language of mathematical geometry in his Location series, in which Platonic-type geometric forms are presented accompanied by labyrinthine poetic-instructional texts.
In order for the diagrams of geometry to function, a number of assumptions must first be made so that they can be said to represent the underlying mathematics. For example, a point of ink on paper is taken to represent a conceptual mathematical point of zero dimensions, and an ink line is understood as representing a perfect one-dimensional line of zero width.
Such paradoxical ambiguities are simply overlooked during the reading of such images, and the American Philosopher and Semiologist Charles Sanders Peirce referred to such inconvenient physical qualities as "accidental characters that have no significance”. (5)
The location of six geometric figures (circle, square, triangle, rectangle, parallelogram and trapezoid).
1974, Set of six etchings, Edition of 25 10 AP.
Sol LeWitt uses the high-fidelity, low-entropy notation of geometry, but contrasts it with a convoluted textual description of, or instructions for, each of his six geometric diagrams. He also chose to write the texts using everyday language rather than the efficient and specialised symbols of mathematics, and the result is a single sentence, hundreds of words long and almost impossible to mentally reconstruct.
(circle, square, triangle, rectangle, parallelogram and trapezoid).
1974, Set of six etchings, Edition of 25 10 AP.
The texts accompanying each geometric image become almost religious mantras, where meaning is lost within the sounds of the words themselves. This fascinating juxtaposition of text and pure notation results in a poetic resonance that is "Romantic-Objective" as well as diagrammatic in nature:
A circle whose radius is equal to half the distance between two points, the first point is found where two lines would cross if the first line were drawn from a point halfway between a point halfway between the center of the square and the upper right corner and the midpoint of the topside to a point halfway between a point halfway between the center of the square and the midpoint of the right side and a point halfway between the midpoint of the right side and the lower right corner, the second line of the first set is drawn from a point halfway between a point halfway between the center of the square and a point halfway between the midpoint and the left side and the upper left corner and the midpoint of the left side to a point halfway between a point halfway between the center of the square and the upper right corner and a point halfway between the midpoint of the right side and the upper right corner; the second point is found where two lines would cross if the first line is drawn from a point halfway between a point halfway between the center of the square and the midpoint of the bottom side and a point halfway between the center of the square and the lower left corner to a point halfway between the end of the first line of the first set and the end of the second line of the first set, the second line of the second set is drawn from a point halfway between the point where the first two lines have crossed and a point halfway between the start of the first line of the first set and a point halfway between the midpoint of the left side and the upper left corner to a point halfway between the end of the first line of the second set and the midpoint of the bottom side; all whose center is located equidistant to three points, the first of which is located at the center of the square, the second point is located at a point halfway between a point halfway between the center of the square and the upper left corner, the third point is located halfway between the start of the first line of the first set and the end of the first line of the second set.
Importantly, LeWitt himself once remarked that he considered his Location series his “poetry”. (7)
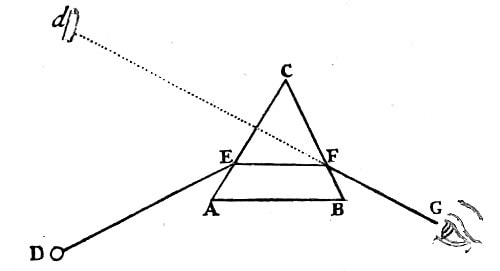
(also known as the ‘Theme Sheet’) (detail)
c. 1448, pen and ink, Windsor Castle, The Royal Collection.
" The triangle abc is similar to a third of the large triangle dbf because it is made up of two equal parts, that is abe and bec, and the large triangle is made up of 6 parts, and each of these parts is equal to each of the said 2, and the 6 parts are these: dec and ced and so on, in similar parts. And if the triangle abc had its sides similar to its axis, cb, the triangle dbf would receive in itself 4 of these triangles, whereas at present it receives 3; thus to see the difference from one of the triangles which are ¼ of the large one and one of those which are ⅓, have the large triangle divided in to twelfths, and say that it is 12 twelfths. Then say that the triangle which is a ⅓ of it is 4 of these twelfths and the triangle that is a ¼ of this large one contains three of these twelfths, so that the difference between 4 and 3 is one twelfth, whence we can say that the smaller is ¾ of the larger. "
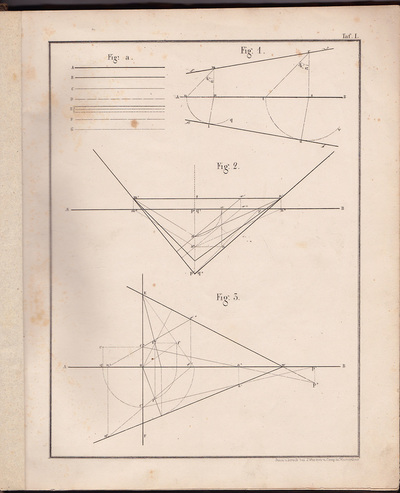
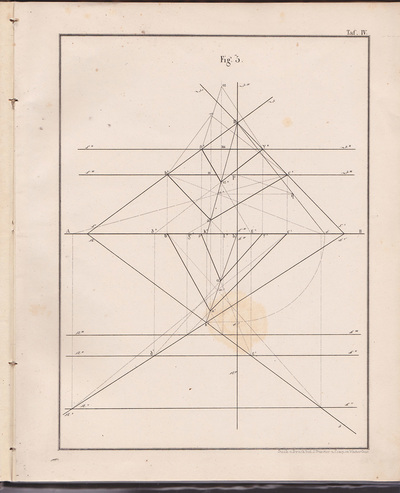
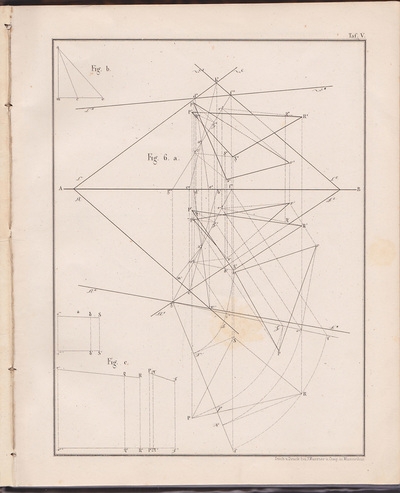
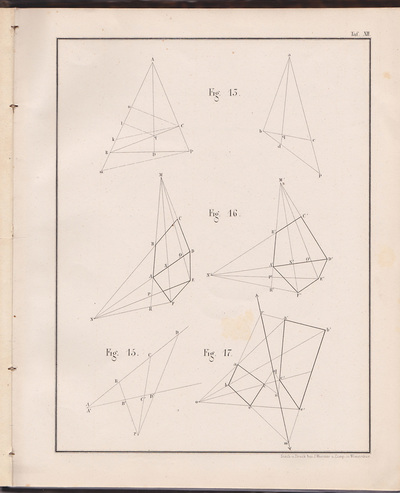
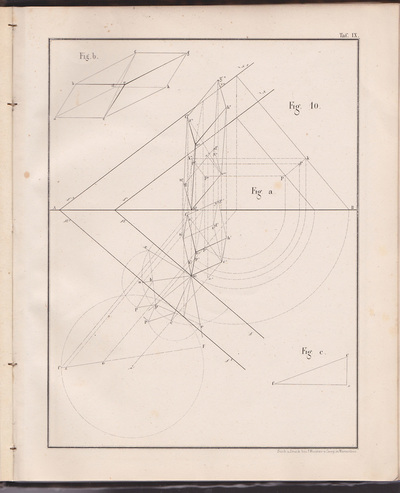
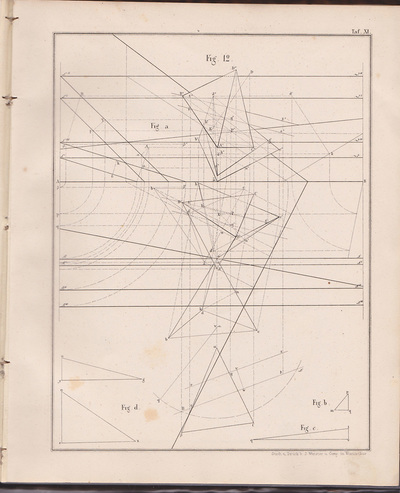
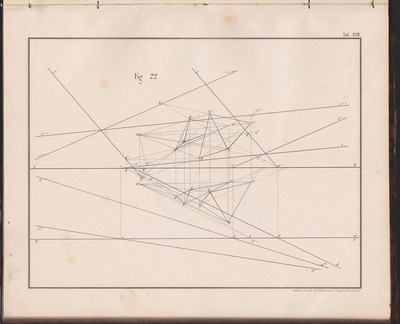
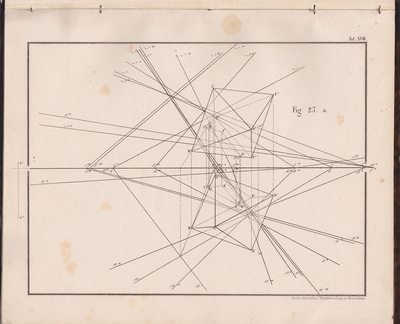
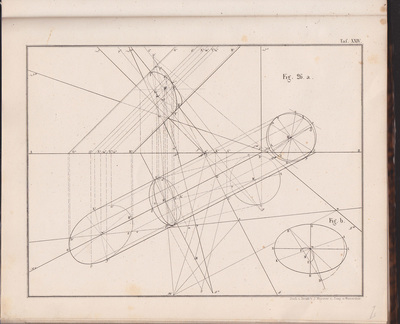
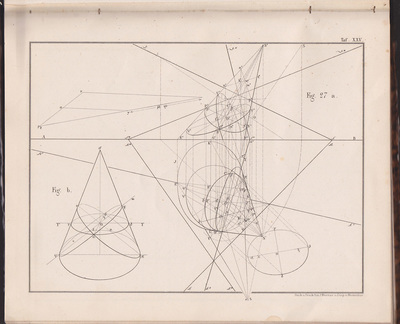
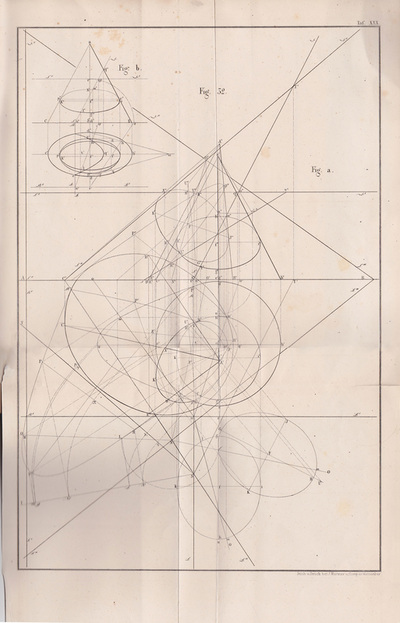
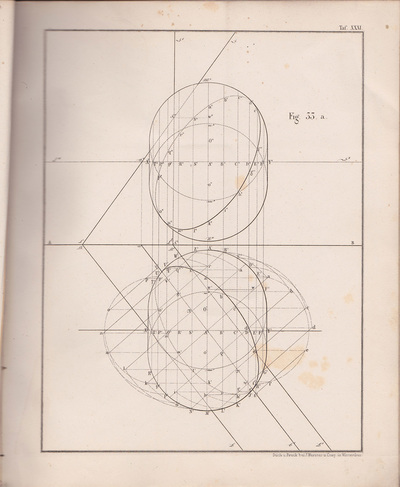
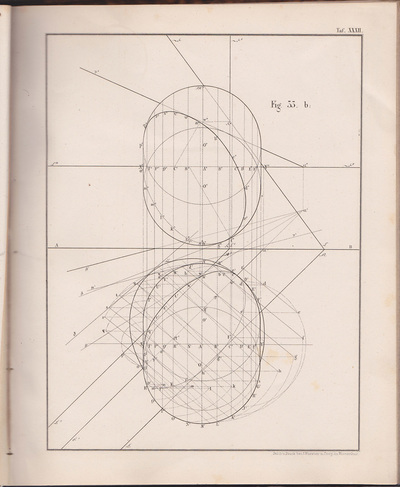
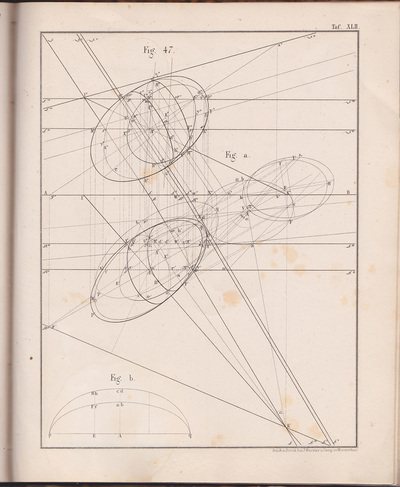
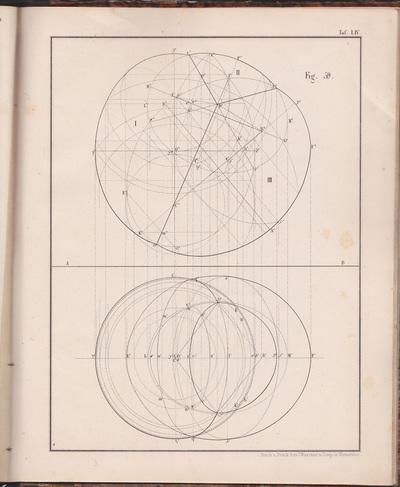
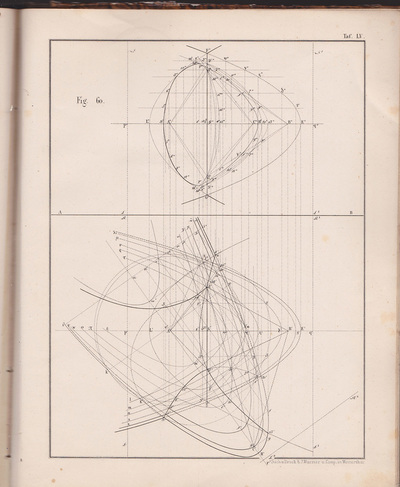
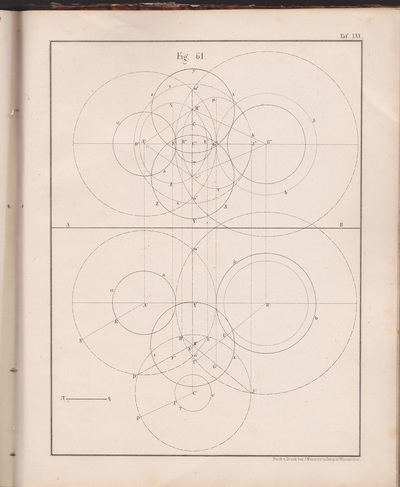
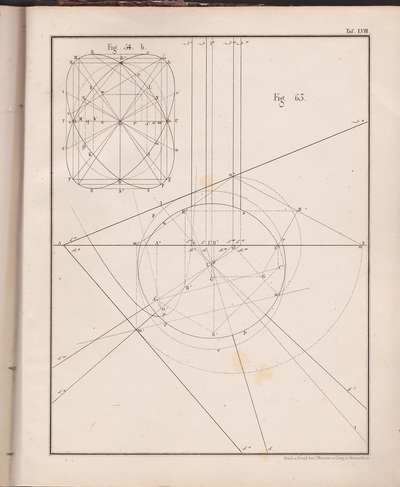
The following selection of geometry diagrams are taken from the beautifully designed German book "der Geometrie descriptive" c.1865, by Leopold Mossbrugger. Fig.a in image 3, presents the various line types employed during the construction of these ideal types of mathematical forms, and the diagrammatic systems used to bring them into being as two dimensional lithographs upon the page.
This particular copy was purchased from an antiquarian bookstore in Prague, the capital the Czech Republic, in 2002
.
by Leopold Mossbrugger, c.1865
References:
1) LeWitt, S. (1967) Paragraphs on Conceptual Art. Art Forum. June, 1967
2) Ibid
3) LeWitt, S. (1969) Sentences on Conceptual Art. In: Art and Language, No. 11. (May 1969) p. 11
4) Celant, G. (2009) (First published:1988) The Sol LeWitt Orchestra. In: Sol LeWitt: 100 views. Eds. Markonish, D. and Cross, S. MASS MoCa in association with Harvard University Press, p. 27.
5) de Waal, C. (2013 ) Peirce: A guide for the perplexed, London: Bloomsbury Academic. p.88.
6) Baume, N. (2001) Sol LeWitt: Open cubes. Exhibition Catalogue. Hartford: Atheneum Museum of Art.
7) Lewitt, S. quoted in: LeWitt and Miller Keller, A. Excerpts from a Correspondence, 1981 – 1983. In: Suzanne Singer, ed., Sol LeWitt wall drawings, 1968 – 1984. Amsterdam: Stedelijk Museum, Eindhoven: Van Abbemuseum, Hartford: Wadford Atheneum, 1984. p. 18-25.
Dr. Michael Whittle
British artist and
researcher based
in Macau
Categories
All
Alchemical Art
Anatomy
Arakawa And Gins
Architecture
Bauhaus
Contemporary-art
Contemporary-art
Duchamp
Genetics
Geology
Geometry
JMW Turner
Leonardo Da Vinci
Literature
Mathematics
Medieval Art
Musicology
Oskar Schlemmer
Perspective
Physics
Romanticism
Sol LeWitt
Surrealism
Theatre
Archives
April 2024
December 2023
November 2023
September 2023
June 2022
June 2021
August 2020
October 2019
August 2018
January 2018
November 2017
October 2017
April 2017
November 2016
October 2016
September 2016
June 2016
May 2016
April 2016
March 2016