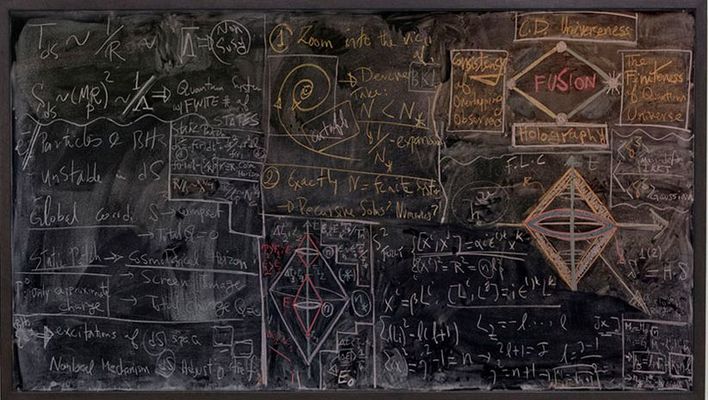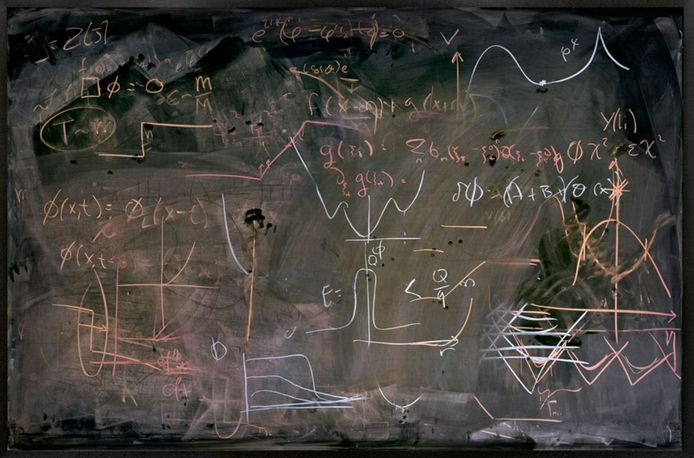|
❉ Blog post 14 on diagrams in the arts and sciences considers the role of diagrams in theoretical and particle physics, as powerful conceptual tools to gain unexpected insights in to the fundamental nature of reality. Figure 1: Lecture scene from the Coen Brother's Academy Award winning file 'A serious Man', 2009. The previous blog looked at some of the difficulties involved in diagramming ideal geometric forms in mathematics, and how the natural limits to human vision affects the accuracy of their interpretation. Despite such shortcomings, diagrams still play an extraordinary variety of roles at the frontiers of mathematical knowledge production, where they help fathom some of the most complex patterns the human minds is capable of comprehending. Mathematician, astronomer and physicist C.F. Gauss famously asserted that: "Mathematics is the Queen of the Sciences, and Arithmetic the Queen of Mathematics. She often condescends to render service to Astronomy and other natural sciences, but under all circumstances the first place is her due." (1) This notion of mathematics in service to science is most discernible in the intimate relationship between maths and physics. In the introduction to Eric Temple Bell's book 'Mathematics - Queen and Servant of Science', titled in reference to Gauss, we're reminded how important advances in pure mathematics have sometimes found application many years after the initial discoveries were made. Without the non-Euclidean Geometry that Riemann developed in 1854, for example, Einstein would have been unable to state his theory of General Relativity and Gravitation in 1916. While mathematics may still retains a position of sovereignty within contemporary science, the relationship is no longer so one sided. Research in contemporary physics has developed such a rich and sophisticated mathematical language of its own that it's quite capable of inspiring insights within the field of mathematics itself. The sheer complexity of the calculations involved in string theory for example, lead physics titan Edward Witten to describe them as a bit of 21st century physics that somehow dropped into the 20th century. Witten's own work in string theory was revolutionary and led Witten to mathematical results so profound that he become the first physicist to be awarded the Fields medal for mathematics in 1990. With this in mind, this blog entry considers some of the most profound, mysterious and powerful diagram in physics, diagrams which seem to transcend their mathematical origins and function at meta-levels in terms of their efficiency and the value of their insights. The first and most iconic example of such diagrams is the Feynman diagram, named after the American physicist Richard Feynman (1918-88). Feynman was the eccentric 'genius's genius' with a legendary reputation for creative problem solving and the ability to teach the complexities of quantum physics to students and non-physicists.
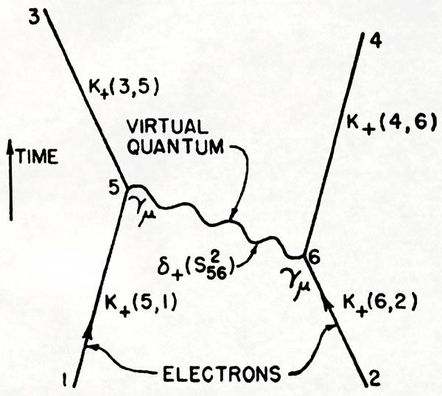
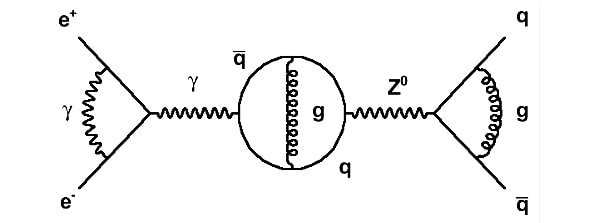
The points where one line connects to another is known as a vertex, and this is where the particles meet and interact: by emitting or absorbing new particles, deflecting one another, or changing type. The Feynman diagram in figure 2 sketches out a map of the mathematical expression: e 2 ∫∫d4 x5 d4 x6 K+(3,5)K+(4,6)γµδ+(s 56 2 )γµK+(5,1)K+(6,2). In it's simplest interpretation two electrons interact, trade a virtual photon and then scatter as a result of their interaction. Figure 3: Richard Feynman with his family in front of his 1974 Dodge Tradesman van, which he decorated with hand painted Feynman diagrams. The visual clarity and precision of feynman diagrams belies the quantum uncertainty of the subatomic collisions and scatterings events they depict. Unlike a bubble chamber image, only the sum of all the Feynman diagrams represent any given particle interaction; particles do not opt for a one diagram or another each time they interact. At the quantum level particles interact in every way available to them, and so an exact description of the scattering process involves summing up a large number of diagrams, each with their own mathematical formula for the likelihood they will occur. In this way a single Feynman diagram represents all possibilities of an interaction from its initial to final state, and so the connections of a Feynman diagram are more important than the configuration of it's lines, squiggles, loops and dashes. Pioneer of data visualization and expert on information graphics Edward Tufte, had 120 Feynman diagrams constructed in stainless steel (see figure 4). His wall mounted constructs represent all 120 different ways that a 6-photon scattering event can be depicted. Figure 4: All possible 6-photon scattering (120 space-time Feynman diagrams), 2012, Edward Tufte, Wall mounted installation of stainless steel with shadows, 530 x 230 x 10 cm (Installation view at Fermilab) Feynman introduced his ingenious schematic in 1948, but by the 1980's their limitations were starting to become apparent, and Feynman himself went on to prove that the diagrams were only approximations that involved an enormous amount of redundancy that arose from their reliance on involving virtual particles (see figure 2). Feynman diagrams were designed to describe all the possible results of subatomic particle collisions, but even a seemingly simple event like two gluons colliding to produce four less energetic gluons, involves some 220 diagrams. Such collisions occur billions of times a second during experiments carried out using modern day particle accelerators. In the mid-2000s patterns began to emerge from events recorded in particle accelerators that repeatedly hinted at an unknown, underlying, coherent mathematical structure. A new set of formulas were proposed by the physicists Ruth Britto, Freddy Cachazo, Bo Feng and Edward Witten, known as the BCFW recursion relations after their discoverers. The formulas dispense with familiar variables of Feynman diagrams such as position and time, and involves an entirely new diagrammatic system first developed in the 1970's by Roger Penrose, named twistor diagrams.
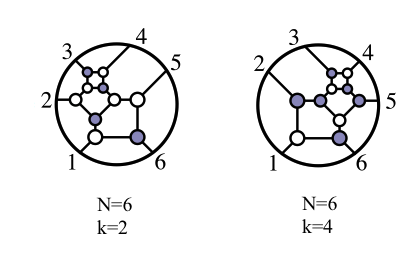
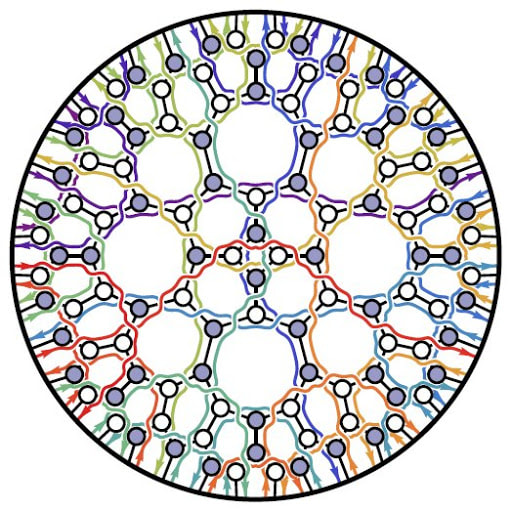
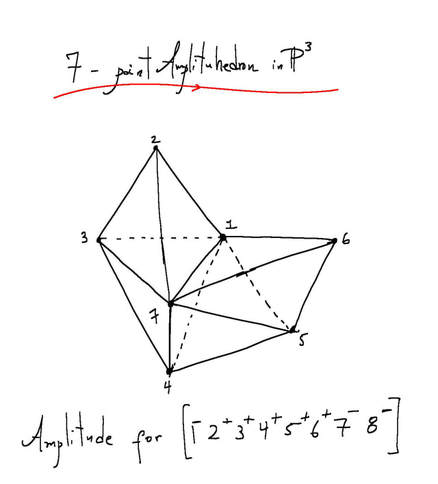
The incredible simplicity and power of twistor diagrams gave them an air of mystery according to Arkani-Hamed: “The terms in these BCFW relations were coming from a different world, and we wanted to understand what that world was.” (3) After over a decade of research with his collaborators, Arkani-Hamed showed how twistor diagrams could be pieced together to create a timeless, multidimensional object known as an 'Amplituhedron' (figure 6). Figure 6: 'On-shell diagrams' are a new visual system for guiding and structuring the calculations of what happens when physical 'on-shell' particles interact, as opposed to the 'off-shell' virtual particles of Feynman diagrams. The Amplituhedron has been described as an intricate, multi-faceted, higher dimensional jewel at the heart of quantum mechanics, a meta-level Feynman diagram completely new to mathematics.
From Feynman diagrams to twistor diagrams and the discovery of the enigmatic amplituhedron, diagrams remain a powerful, albeit mysterious tool in theoretical physics. They permit information to be stored and shared with high fidelity, but they also mobilise and shape new knowledge by allowing intuition and rational thought to play a role in the creative process. Diagrams in actions - the photography of Alejandro Guijarro Alejandro Guijarro, STANFORD III, 2012, C-type print, 117 x 240 cm For his 'Momentum' series (2010-2013), Spanish photographer Alejandro Guijarro traveled to several international academic institutions that specialize in quantum mechanics: CERN, Stanford, Berkeley and Oxford. In a form of documentation, Guijarro measured and photographed blackboards that he found in lecture theatres, meeting rooms and offices, then printed the images at a 1:1 scale. The series highlights the transitive nature of diagrams at work during the creation and transmission of knowledge. It presents the process as a physically involved gestural performance, as various trains of thought are followed and erased to leave a blurred palimpsest. 'Momentum' is reminiscent of Marcel Duchamp’s project 'Unhappy Readymade', discussed in this previous Blog: The Diagrams of Geometry part II- A soggy book of diagrams as a wedding present from Marcel Duchamp. Both projects present us with a token of something lost - information and knowledge made manifest through the substrates ink, paper, chalk and board only to be subject to entropy. In the case of 'Unhappy Readymade' it's the wind and rain which add entropy, in the case of Guijarro’s 'Momentum' it's the hand of the professor, janitor or the student armed with a blackboard eraser that return the arena of ideas to a tabula rasa. Alejandro Guijarro, BERKLEY II, 2012, C-type print, 112 x 236 cm Alejandro Guijarro, CAMBRIDGE VII, 2011, C-type print, 120 x 300 cm Alejandro Guijarro, BERKELEY VIII, 2011, C-type print, 117 x 174 cm Alejandro Guijarro, SLAC V, 2012, C-type print, 117 x 180 cm Alejandro Guijarro, SLAC V, 2012, C-type print, 117 x 180 cm Alejandro Guijarro, OXFORD I, 2011, C-type print, 110 x 150 cm Notes:
1) C.F. Gauss quoted in Gauss zum Gedächtniss (1856) by Wolfgang Sartorius von Waltershausen 2) Andrew Hodges, Online at: http://www.twistordiagrams.org.uk/papers/ 3) Arkani-Hamed, quoted in 'A Jewel at the Heart of Quantum Mechanics' by Natalie Wolchova, online at: https://www.quantamagazine.org/physicists-discover-geometry-underlying-particle-physics-20130917/ 4) Jacob Bourjaily, quoted in 'A Jewel at the Heart of Quantum Mechanics' by Natalie Wolchova, online at: https://www.quantamagazine.org/physicists-discover-geometry-underlying-particle-physics-20130917/
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Dr. Michael WhittleBritish artist and Posts:
Categories
All
Archives
April 2024
|